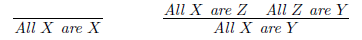
「可靠性」(soundness)和「完備性」(completeness)是兩個與「邏輯系統」相關的重要元邏輯性質(metalogical property),一個邏輯系統最好能同時具備這兩種性質。為證明一個邏輯系統具備這兩種性質,往往需要使用不同的證明策略。學過數理邏輯的讀者都應知道,謂詞邏輯(自然演繹系統)的完備性證明比可靠性證明長而複雜(例見Yaqub (2015)),其長度足以令初學者望而生畏,其複雜性也令初學者暈頭轉向。本文主旨是透過一個極為簡單的邏輯系統展示可靠性證明與完備性證明的差異(註1)。
本文介紹的邏輯系統是只包含量詞all的系統,故稱L(all),這個系統的基本詞匯只有謂詞A、B、X、Y等。把這些謂詞填入語句框架「All ... are ...」的...,便可構成語句,如All A are B、All X are Y等(請注意在這個系統中,all和are並非獨立的詞匯)。這個系統包含下圖所示的兩條「推理規則」(rule of inference):
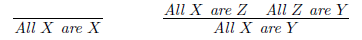
上圖中的X、Y和Z代表任意謂詞。此外,上圖中的兩條推理規則都包含一條橫線,這條橫線可以粗略地看成代表「推導」,即可以從橫線上的(零個或兩個)語句推導出橫線下的語句。第一條規則代表我們可以「無中生有」地推導出任何形如All X are X的語句,例如All A are A等(註2)。第二條規則則代表,我們可以從語句All X are Z和All Z are Y推導出All X are Y。
通過重複運用以上兩條規則,便可從給定的稱為「前提」(premise)的語句推導出稱為「結論」(conclusion)的語句。以下我們使用式子
代表可通過運用L(all)中的推理規則,從前提集合Σ推導出結論p。在上式中,我們也說p是Σ的「語形後承」(syntactic consequence),或者說從Σ到p的推論是「可證明」(provable)的。舉例說,下圖展示在L(all)下從前提集合{All Q are A, All A are B, All B are D}推導出結論All Q are D的「證明樹」(proof tree):
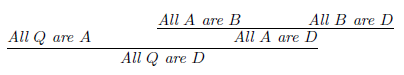
我們可以把上面的事實記作:
在一個推論中,前提集合可以是空集。根據上面第一條推理規則,在L(all)中,無需任何前提也可推導出結論All A are A,我們可以把這個事實記作(其中Φ代表空集):
接著介紹「模型」(model)的概念。L(all)的任何一個模型M由以下兩個要素組成:「論域」(universe)(以下記作UM)和「釋義函數」(interpretation function)(用|| ||M代表),即若T是某個語句/謂詞,則||T||M是這個語句/謂詞在模型M下的釋義。論域是由個體組成的集合。若p和A分別是語句和謂詞,則||p||M等於語句p的真值(用1和0分別代表「真」和「假」),||A||M則是由UM的部分成員組成的某個集合(亦即UM的某個子集)。在L(all)中,語句All A are B的釋義(即真值)不是任意確定的,而是取決於所包含謂詞A和B的釋義,以下是All A are B的釋義與A和B的釋義之間的關係(註3):
請注意L(all)可以有不只一個模型,因此同一個語句/謂詞在不同模型下可以有不同的釋義。舉例說,設有模型M,並且在這個模型中,UM = {a, b, c},||A||M = {a}和||B||M = {a, c}。那麼根據(4),由於||A||M ⊆ ||B||M,我們有||All A are B||M = 1。現在又設有另一個模型N,並且在這個模型中,UN = {u, v, w},||A||N = {u, v}和||B||N = {v, w}。那麼根據(4),由於||A||N ⊈ ||B||N,我們有||All A are B||N = 0。
運用(4),同樣可從給定的前提推導出結論。以下我們使用式子
代表就任意模型M而言,若前提集合Σ中所有語句在M下的真值都是1,那麼也有||p||M = 1。在上式中,我們也說p是Σ的「語義後承」(semanic consequence),或者說從Σ到p的推論是「有效」(valid)的。舉例說,設給定前提集合{All Q are A, All A are B, All B are D},並設就任意模型M而言,這個集合中的三個語句在M下的真值都是1,由此根據(4),我們有以下三個集合論命題:||Q||M ⊆ ||A||M,||A||M ⊆ ||B||M和||B||M ⊆ ||D||M。根據子集關係⊆的傳遞性,從以上三個集合論命題,可推導出||Q||M ⊆ ||D||M。由此根據(4),可知||All Q are D||M = 1。以上事實可以記作
如前所述,在一個推論中,前提集合可以是空集。舉例說,根據子集關係⊆的自反性,我們知道在任何模型M下,都有||A||M ⊆ ||A||M。由此根據(4),可知||All A are A||M = 1。由於上述結論是在沒有前提的情況下推導出的,我們把這個事實記作:
雖然(2)和(6)(以及(3)和(7))這兩個推論有相同的前提集合和結論,但兩者的推導方法很不同:(2)(以及(3))的推導是純形式的,即純粹根據給定前提的形式和L(all)中的推理規則進行推導,而無須理會前提和結論中詞項的釋義;(6)(以及(7))的推導則須依賴於(4)中對語句All A are B的釋義,以及集合論中有關⊆的性質的知識,而以上這些釋義和集合論知識都跟前述推理規則沒有直接關係。
現在我們可以定義邏輯系統L(all)的可靠性和完備性如下。L(all)是可靠的,若對任何前提集合Σ和結論p,都有
L(all)是完備的,若對任何前提集合Σ和結論p,都有
上述定義也可概括為,L(all)是可靠的,若任何可證明的推論都是有效的;L(all)是完備的,若任何有效的推論都是可證明的。
接下來證明上述兩個元邏輯性質,首先考慮可靠性。如要像Yaqub (2015)證明謂詞邏輯(自然演繹系統)的可靠性那樣對L(all)的可靠性進行嚴格證明,須引入很多與數學歸納法和證明樹有關的技術細節。若撇除這些細節,L(all)可靠性的證明實質上就是對L(all)兩條推理規則的有效性的證明,所以以下將集中證明上述兩條推理規則的有效性,即證明Φ |= All X are X和{All X are Z, All Z are Y} |= All X are Y。但在前面推導(6)和(7)時,我們實質上是在證明這兩條推理規則的特例的有效性,因此只需把前面的證明推廣到一般情況便可以。
具體地說,首先,根據子集關係⊆的自反性,我們知道在任何模型M下,都有||X||M ⊆ ||X||M。由此根據(4),可知||All X are X||M = 1。由於上述結論是在沒有前提的情況下推導出的,我們有Φ |= All X are X,由此可知L(all)的第一條推理規則是有效的。其次,設給定前提集合{All X are Z, All Z are Y},並設就任意模型M而言,這個集合中的兩個語句在M下的真值都是1,由此根據(4),我們有以下兩個集合論命題:||X||M ⊆ ||Z||M和||Z||M ⊆ ||Y||M。根據子集關係⊆的傳遞性,從以上兩個集合論命題,可推導出||X||M ⊆ ||Y||M。由此根據(4),可知||All X are Y||M = 1。我們可以把上述推論結果寫成{All X are Z, All Z are Y} |= All X are Y,由此可知L(all)的第二條推理規則也是有效的,L(all)的可靠性乃得證。
其次考慮完備性。完備性的證明往往比可靠性的證明困難,以下引述Moss (2008)對L(all)完備性的證明(註4)。讀者將會看到,這個證明引入了一個特殊的釋義函數,這種情況跟Sider (2010)在證明命題邏輯(公理系統)的完備性時引入了一個特殊釋義函數很相似。為證明(9),首先假設Σ |= All X are Y。接著定義一個模型M,這個模型的論域是UM = {a},即只包含一個個體a的「單元集」(singleton);以下是這個模型的釋義函數|| ||M的部分定義(註5)(在以下定義中,Z是任意謂詞,Σ和X與前述假設Σ |= All X are Y中的Σ和X相同):
| ||Z||M = | {a}, | 如Σ |− All X are Z | (10) |
| Φ, | 如屬其他情況 |
請注意上述定義沒有遺漏||Z||M的任何可能值。由於M的論域只有一個元素a,在M下任何謂詞Z的釋義只有兩個可能:要麼等於{a},要麼等於空集。
接著證明一個事實:若Σ包含語句All V are W,則必有||V||M ⊆ ||W||M。為此,假設Σ包含語句All V are W以及||V||M ≠ Φ (否則必有||V||M ⊆ ||W||M,因為空集是任何集合的子集),因此||V||M = {a}。由此根據(10),必有Σ |− All X are V。這即是說,在L(all)下,可以從前提集合Σ推導出All X are V。但前面假設Σ中還有All V are W,把這個語句跟All X are V放在一起(位於其右側),便可根據第二條推理規則推出All X are W。這即是說,在L(all)下,可以從前提集合Σ推導出All X are W,亦即Σ |− All X are W。由此根據(10),必有||W||M = {a},故有||V||M ⊆ ||W||M。
根據(4),上段證得的事實等同於,Σ中的任何語句All V are W都滿足||All V are W||M = 1。由此根據前述假設Σ |= All X are Y,可知必有||All X are Y||M = 1。由此根據(4),必有
另一方面,根據第一條推理規則,我們有Φ |− All X are X,由此也有Σ |− All X are X (註6)。由此根據(10),必有||X||M = {a}。由此根據(11),必也有||Y||M = {a}。由此再根據(10),必有Σ |− All X are Y。至此證得若Σ |= All X are Y,則Σ |− All X are Y,L(all)的完備性乃得證。
最後總結L(all)可靠性和完備性證明的差異。上述可靠性證明實質上是證明兩條推理規則的集合論依據,證明中只需應用簡單的集合論知識,所以較為直觀。上述完備性證明卻並不直觀,上面在假設Σ |= All X are Y後,並不直接證明如何運用L(all)的兩條推理規則從Σ推導出All X are Y,而是借助釋義函數(10)去間接證明這一點。整個證明的難點就是構造這個釋義函數(10),因為這是一個很特殊的函數,它在語義概念中揉合了語形概念(註7)。如非看過這個證明,一般人如何能構想出這樣的函數?總括而言,可靠性證明一般較為直觀,而完備性證明則常常需要一些奇思妙想。


