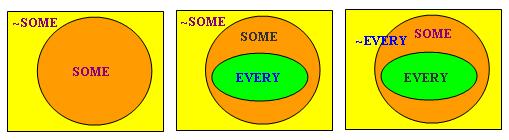
「自然邏輯」(Natural Logic)是指以貼近自然語言的表達式為基礎的邏輯推理。古希臘的形式邏輯主要研究量化句之間的推理關係,所謂「量化句」,是指形如「所有S都是/不是P」和「有(至少一個)S是/不是P」的命題。這些量化句是從自然語言歸納出來的,具有一般句子的「主謂」(Subject-Predicate)結構,因此古典形式邏輯可稱為「古典自然邏輯」。古典形式邏輯的自然主義風格反映了西方早期邏輯學與語言學的密切關係,事實上,「主語」和「謂語」便既是邏輯學,又是語法學的術語。
「古典自然邏輯」主宰西方邏輯學兩千年,及至19世紀末20世紀初,西方興起了現代數理邏輯,邏輯學發生了「數學轉向」,大量引進數學方法。其最重要分支—「一階謂詞邏輯」(First Order Predicate Logic)在20世紀取得空前成功,在深度和廣度兩方面均大大超越古典邏輯。事實上,現代數理邏輯是以數學概念而非自然語言作為研究對象,背離了古典邏輯學與語言學緊密相連的傳統。此外,古典邏輯的研究結果由於可在一階邏輯下得到更有系統和更嚴格的解釋,完全可被歸併入一階邏輯,因而喪失了特殊性;而且現代數理邏輯還包括很多古典邏輯所沒有的內容,新興的邏輯學家不再使用或研究古典邏輯的各種術語和範疇,古典邏輯似乎已被掃進了歷史的垃圾堆中。
可是,物極必反,從20世紀中期起,自然邏輯重又引起部分學者的興趣,這主要有兩方面的原因。首先,當代是學術界空前繁榮、百花齊放的時期。不僅處於「正統」地位的數理邏輯獲得長足發展,各種「非正統」邏輯也如雨後春筍般應運而生,及至21世紀初最終形成試圖集各派大成的「泛邏輯」(Universal Logic)思潮。自然邏輯作為有悠久歷史傳承的邏輯流派,自然也得以「死灰復燃」。
其次,一階謂詞邏輯有其局限性,主要表現為其「非自然性」、「表達力」不足和「不可判定性」。由於早期的數理邏輯學家認為自然語言不精確和充滿歧義,他們致力發展專門為數理邏輯而設的「人工符號語言」。雖然這套語言對研究數學推理十分有用,但對研究日常語言的推理卻顯得格格不入。舉例說,簡單的一句
在一階謂詞邏輯中卻要表達為
上式用日常語言繙出來就是
比較一下(1)和(3),便可見後者是多麼累贅和不自然,這是因為(2)完全沒有反映(1)的「主謂」結構,也沒有表示數字2的簡便方法。一階謂詞邏輯還有「表達力」(Expressive Power)不足的缺點,例如這種邏輯便無法表達下句:
鑑於「超過一半」在日常語言中是很常用的量詞,由此可見一階謂詞邏輯實在不適合用來研究自然語言的推理。
至於一階謂詞邏輯的「不可判定性」(Undecidability),是指不存在一套可在有窮時間內完成的「算法」(Algorithm),可用來判斷任意一階邏輯推理是否有效。換句話說,我們無法把一階邏輯推理完全變成一種可交由電腦代勞的機械運算,很多有效的推理模式仍有待人們去研究和發掘。
正由於存在上述局限性,數理邏輯無法涵蓋自然語言中所有有效的邏輯推理,因此一些對自然語言推理感興趣的學者便轉向對自然邏輯的研究。不過,他們的研究不是重走古典邏輯的老路,而是從全新的角度去研究自然語言推理,形成有別於「古典自然邏輯」的「現代自然邏輯」。
「現代自然邏輯」尚處於初創階段,對於其研究對象,至今未有定論,可謂眾說紛紜。歸納各家的說法,大致上可以把自然邏輯的研究對象定為:以貼近自然語言的表達式為基礎的邏輯推理。對於這個定義,須作兩點說明。首先,這裡是說「貼近自然語言的表達式」而非「自然語言」,這是因為邏輯學作為一種理論概括,不是對無窮無盡的具體推理逐個進行研究,而是從抽象概括的角度研究有限的「推理模式」;這些推理模式往往並非表現為純粹的自然語言句子,而是表現為代表自然語言的「表達式」。以古典邏輯為例,前述的「所有S都是/不是P」便是一種抽象的表達式,其中S和P是「變項」,而「所有」一詞其實也是從日常語言中各種表達「全稱量化」的同義詞(例如「所有」、「每個」、「一切」等)抽象出來的。
其次,「貼近」是一個模糊概念,不同人對此可以有很不同的理解。某些學者所研究的表達式基本上保留了自然語言句子的原貌,只是把其中的「非邏輯詞項」處理成變項(古典邏輯就是這樣做),或者加上某些句法/語義標記(例如Sanchez Valencia)(註1)。以前述的(1)為例,在上述後一種處理方法下,(1)會被表達為:
| (5) | |||
上式的第二行就是句中各個詞項的句法/語義標記。
某些學者則把自然語言句子表達成抽象的代數公式,但跟謂詞邏輯表達式不同,這些公式反映了自然語言句子的「主謂」結構(例如Sommers和Murphree)。在這種處理方法下,(1)會被表達為
其中"2S"和"D"分別對應(1)的主語和謂語。
還有一些學者處於上述兩個極端之間,他們把自然語言句子翻譯成某種語義學理論的表達式,這些表達式盡量保留句子的原貌。Keenan是這方面的代表,他使用「廣義量詞理論」的框架,而廣義量詞理論曾被稱為「主謂邏輯」,因為它保留了自然語言句子的「主謂」結構,例如把(1)表達為
其中"(at least 2)(STUDENT)"和"DANCE"分別對應(1)的主語和謂語。綜上所述,不同學者對何謂「貼近自然語言」可以有不同的解讀,本文採取兼容的態度,把以上這些理論都歸入「現代自然邏輯」的範圍。
現代自然邏輯繼承了古典邏輯的傳統,主要關注量化句的推理問題。不過跟古典邏輯不同,現代自然邏輯研究的量詞已不限於傳統的「所有」和「有(至少一個)」,而是「廣義量詞」(Generalized Quantifier)。有關廣義量詞的詳細介紹,請參閱拙著「廣義量詞系列」。簡言之,廣義量詞是自然語言中表達集合之間的邏輯/數量關係的眾多手段之一(註2)。在句法學上,不同類型的廣義量詞對應著多種語言結構,本文集中討論最重要的一種-「限定詞」(Determiner),例子如英語的"every"、"some"、"at least one third"、"exactly three"、"all except two"、"John's"、"many"等等。
從廣義量詞理論的角度看,限定詞含有兩個「論元」(Argument),可分別稱為「左論元」(Left Argument)和「右論元」(Right Argument),分別對應著自然語言句子中的主語(略去限定詞後的部分)和謂語。以下筆者將採用Keenan的記法,把限定詞及其兩個論元寫成Q(A)(B)的形式,其中Q、A和B分別代表「限定詞」、「左論元」和「右論元」,例如在(7)中,(at least 2)、STUDENT和DANCE分別是「限定詞」、「左論元」和「右論元」。
涉及廣義量詞的自然邏輯推理豐富多樣,學者只能擇其最重要者進行研究,以下是筆者經整合諸家學說後歸納出來的四大類推理:
以下將分節介紹當代學者對這四大類推理的研究成果。
「單調性」(Monotonicity)是現代數學和邏輯學上很常見的概念,也是廣義量詞理論重點研究的量詞普遍性質之一。對於單調性,廣義量詞理論研究當量詞的論元被換成其「母集」(Superset)或「子集」(Subset)後,該量詞的真值條件有何變化。由於限定詞有左、右兩個論元,相應地也應有兩類單調性,下表給出「左單調性」的兩個次類的定義。在以下定義中,設Q為限定詞,A、A'、B和B'為集合。
| 名稱 | 定義 |
|---|---|
此外,若Q是「左遞增」或「左遞減」的,則Q是「左單調」(Left Monotone)的,否則是「左非單調」(Left Non-Monotone)的。舉例說,"every"就是「左遞減」的,這是因為"every(A)(B)"真當且僅當A ⊆ B,現在如有A' ⊆ A並且A ⊆ B,則必有A' ⊆ B,即"every(A')(B)"真。類似地,我們也可定義「右單調性」的兩個次類。
根據量詞的單調性,我們可以得到各種有效的「單調性推理」(Monotonicity Inference),例如根據上述 "every" 的「左遞減性」,可以得到以下的有效推理:
當代學者對「單調性推理」的研究可粗略地分為三個方向,現分述於下(註3)。
第一個研究方向是確定各類型量詞的單調性。對於論元結構較簡單的量詞(包括限定詞),不難確定其單調性,但對於其他類型的量詞,便要應用較複雜的方法,這方面的研究計有Smessaert (1996)對「結構化量詞」(Structured Quantifier)(例如"More boys than girls sang"中的"more ... than ...")的研究、Zuber (2010)對「迭代量詞」(Iterated Quantifier)(例如"Every boy loves some girl"中的"every ... some")的研究、Peters and Westerstahl (2006)對「所有格結構」(Possessive Construction)(例如"Some of at most 3 members' cars are red"中的"some of at most 3 members' ")的研究等等。
當某些簡單量詞被置於特殊語境下,其單調性會有異常表現,這些特殊語境包括「統指謂詞」(Collective Predicate)(例如"meet"、"do ... together"等)、「內涵謂詞」(Intensional Predicate)(例如"seek"、"wish to"等)和「動態語境」(Dynamic Context)(指包含代名詞跨句指稱現象的語境)。舉例說,下句由於包含「統指謂詞」 "drank ... together" ,"all"喪失了原有的「左遞減性」,導致以下推理無效:
不同學者對上述特殊語境作了不同研究,包括Ben-Avi (2002)對「統指謂詞」的研究、Zimmermann (2006)對「內涵謂詞」的研究、Kanazawa (1994)對「動態語境」的研究等,對這些異常現象作出了解釋。
除了廣義量詞外,某些語言結構也隱含著量化的因素,也可能存在單調性的問題,因而也被列入單調性研究的範圍之內,這方面的研究包括de Swart (1993)對「量化狀語」(Adverb of Quantification) 的研究、Kennedy (1998)對「極性形容詞」(Polar Adjective)的研究、Zwarts and Winter (2000)對「方位介詞」(Locative Adposition)的研究等,其中Zwarts and Winter (2000)更區分了「點單調性」(Point Monotonicity)和「向量單調性」(Vector Monotonicity)的概念,前者表達空間上的包含關係,後者表達空間上的線性次序,例如以下有效推理便是這兩種單調性的體現:
不僅如此,如果我們把量詞看成「高階集合」(註4),那麼量詞之間的蘊涵關係便可看成集合之間的包含關係;而作用於量化句的「命題聯結詞」則可被看成「高階算子」,因此我們也可研究這些「高階算子」的「高階單調性」(Higher Order Monotonicity)。舉例說,對任意集合B和任意非空集合A來說,總有以下蘊涵關係成立:
現在如果我們把"every"和"some"處理成高階集合EVERY和SOME,並把"~"處理成高階算子,那麼上述關係便可表達為下圖:

一般地,對任何高階集合A、A',我們有
由此可見,"~"是一個具有「高階遞減性」的高階算子。其他命題聯結詞也可作類似處理,這裡不擬詳述。
第二個研究方向是把單調性概念加以推廣(Generalization)或精細化(Refinement),這方面的研究有以下三種。自然語言中有一些量詞在某個論元上是非單調的,但如果把量化範圍限制於某個局部範圍內,這些量詞便可能呈現遞增/遞減性,這就是Glockner (2006)提出的「局部單調性」(Local Monotonicity)概念。舉例說,"more than 10%"這個限定詞本是「左非單調」的,但如果限制其左論元須在{S: X ⊆ S ⊆ X ∪ Y}內取值,而其右論元須等於Y (其中X和Y為任意集合),則"more than 10%"在這個局部範圍內是「局部遞增」的。利用上述結果,我們可以得到以下有效推理:
如表1所示,就限定詞而言,單調性可分為四個次類(左/右遞增/遞減),但其實還可以作出更細致的分類。Peters and Westerstahl (2006)提出了六種「基本單調性」(Basic Monotonicity)的概念,其中兩種就是右遞增/遞減性;至於左單調性,則分為四種,分別以東南、西南、西北和東北這四個方向命名。由於這套理論須用到廣義量詞理論中「數字三角形」的概念,這裡不擬詳述,只想指出某些量詞雖然是左非單調的,但在被分解為「基本單調性」後,卻呈現遞增/遞減性質。舉例說,限定詞"at least 1/3"本是「左非單調」的,但從「基本單調性」的角度看,卻是「東南方向遞增、東北方向遞減」的。利用這個結果,我們可以得到以下有效推理:
「單調性」與三種「布爾運算」(即集合論上的「并」、「交」、「補」和邏輯學上的「或」、「和」、「非」)存在微妙的關係,例如容易證明,Q是右遞增的當且僅當對任何A、B、B',都有
現在如果把上式中的"⇒"改為"⇔",我們將得到一種新的性質,稱為「右可乘性」。請注意如果Q是右可乘的,則Q必是右遞增的,因此「右可乘性」可被看成「右遞增性」的次類。由此我們看到,透過研究單調性與三種布爾運算的各種關係,我們將可得到單調性的各種次類,筆者把這些次類統稱為「加乘性質」(Additivity / Multiplicativity)和「廣義德.摩根性質」(Generalized de Morgan Property),這正是Zwarts (1997)和van der Wouden (1997)的研究課題。舉例說,根據"every"的「左反加性」(註5),我們有以下有效推理:
第三個研究方向是建構有關「單調性演算」(Monotonicity Calculus)的理論。在一個結構複雜的句子中,任一短語可能處於多個量詞或否定詞的轄域之內,這個短語的單調性會受到這些量詞或否定詞的影響,「單調性演算」的目的就是設計一套規則或算法,用來確定一個複雜句中各個短語的單調性,並由此作出推理。
Sanchez Valencia (1991)以「證明論語義學」(Proof-Theoretic Semantics)和「範疇語法」(Categorial Grammar)為基礎設計了第一個「單調性演算」模型,其具體操作方法是,先為句子中的各個詞項加上適當的「範疇語法-單調性」標記,然後借助這些標記逐步算出各個詞項的單調性。以下用一個簡單的例子以作說明,試考慮句子
下圖顯示這句的「計算樹」:

我們可以把上述計算看成如下的配對過程:找出相鄰的一對形如"Am → B"和"A"的標記(其中"m"代表單調性標記,可以取"+"號、"−"號或零標記;在配對時不須理會"A"是否有括號),在"Am → B"下加上"+"號,並在"A"下加上"m",然後把"Am → B"和"A"合併為"B"。上述配對過程須一直進行下去,直至最後所得標記是"t"為止。舉例說,在上圖中,"didn't"的標記為"(e→t)− → (e→t)",而"arrive early"的標記為"e→t",兩者正可配對,因此我們在"didn't"的標記下加上"+"號,並在"arrive early"的標記下加上"−"號,然後把兩者合併為"e→t"。
完成上述過程後,便可確定各個詞項的單調性如下:若從「計算樹」樹根的"t"到達該詞項的路徑上有任何零標記,該詞項就是非單調的;若路徑上有偶數個"−"號,該詞項是遞增的;若路徑上有奇數個"−"號,則該詞項是遞減的。根據上圖,可知在(8)中"students"和"arrive early"分別是遞減和遞增的,由此可得到以下推理:
繼Sanchez Valencia (1991)之後,Dowty (1994)、Kas and Zwarts (1994)、Bernardi (2002)、Fyodorov (2002)、Zamansky (2004)、van Eijck (2007)等人繼續以範疇語法為基礎提出各種模型,以改良Sanchez Valencia (1991)的模型或把其結果推廣應用於其他範疇,例如Kas and Zwarts (1994)的「擴充單調性演算」(Extended Monotonicity Calculus)模型便是以比「單調性」更細致的「加乘性質」作為計算目標,其研究目標不是推導單調性推理,而是解決「極性敏感詞」(Polarity Sensitive Item)的語法問題。
除了範疇語法外,其他類型的推理系統也被用來作為單調性演算的基礎,例如Geurts (2003)的「自然演繹」(Natural Deduction)模型以及MacCartney (2009)的「自然語言推理」(Natural Language Inference)模型(屬於「計算語義學」Computational Semantics的範疇),其中MacCartney (2009)的模型不僅包含單調性演算的內容,還包含「廣義對當關係」推理(詳見下文)的內容。
上述諸理論都可歸入「證明論語義學」的範疇,除此以外,也可從「模型論語義學」(Model-Theoretic Semantics)(註6)的角度研究單調性演算,周家發(2006)便是這方面的例子。周家發(2006)以廣義量詞理論為基礎,提出了「單調性推理原理」(Principles of Monotonicity Inferences),其操作方法是先把自然語言句子寫成廣義量詞理論的表達式,然後根據該表達式的轄域結構,確定各個詞項的單調性。以(8)為例,該句可以表達為
根據上式,ARRIVE-EARLY同時處於"(fewer than 10)"和"~"的轄域之內,同時受到這兩個算子的遞減性影響,結果呈遞增性;而STUDENT則只受"(fewer than 10)"的影響,所以呈遞減性,這個分析結果跟前述一致。
有關單調性推理的其他內容,請參閱拙文《廣義量詞系列:單調性推理原理》、《廣義量詞系列:單調性推理的擴展》和
《廣義量詞系列:單調性的進階研究》。
「三段論推理」(Syllogistic Inference)是古典邏輯重點研究的推理,曾經幾乎成為古典邏輯的同義詞。在古典邏輯中,「三段論」(Syllogism)是指由三個命題組成的推理,其中兩個是「前提」(Premise),其餘一個是「結論」 (Conclusion)。根據三個命題的內部結構,古典邏輯學家把三段論區分為不同的「格」(Figure)和「式」(Mood)。此外,古典邏輯還有一個獨特的「周延性」(Distributivity)概念:全稱命題(即包含「所有」的命題)的主語以及否定命題的謂語是周延的,而特稱命題(即包含「有(至少一個)」的命題)的主語以及肯定命題的謂語則是不周延的。
古典邏輯學家的工作就是確定哪些三段論格式是有效推理,例如他們指出以下代號為"Barbara"的推理便是有效的(即以任何詞項代入以下的S、P和M都可得到正確的推理):
| 前提1: | Every M is P. |
| 前提2: | Every S is M. |
| 結論: | Every S is P. |
不僅如此,古典邏輯學家還嘗試以「周延性」概念為基礎,定出一些判斷三段論有效性的簡便規則。
自從現代數理邏輯興起後,三段論推理喪失了獨立研究的價值。其實,即使在現代自然邏輯下,古典三段論也沒有獨立價值,這是因為根據van Eijck (1984, 2005)的研究,古典三段論可以被歸結為單調性推理的特例,而「周延性」則相當於遞減性。舉例說,我們可以這樣理解前述的"Barbara"推理:前提2告訴我們S ⊆ M,由此便可根據前提1以及"every"的左遞減性推出結論。
雖然如此,當代仍有一些學者研究三段論推理,他們採取嶄新的視角,突破古典三段論的某些框框。事實上,當代學者研究的三段論無論在格式、所用的量詞,以至所含命題的數目上,都可以不同於古典三段論,因此本文對「三段論」採取一個極寬鬆的定義:從至少兩個給定的量化句(前提)推出至少一個新量化句(結論)的推理。當代學者對「三段論推理」的研究可粗略地分為三個方向,現分述於下。
第一個研究方向是基本沿襲古典三段論的原有概念,但嘗試把古典三段論推廣至其他量化句,推導出不可歸結為單調性推理的「新三段論」,這些研究計有:Reichenbach (1952)研究的含否定詞的三段論、Thompson (1986)和Peterson (2000)研究的含模糊量詞或分數量詞的三段論、高東平(2006)研究的含模糊量詞的三段論、Cavaliere and Donnarumma (2007)研究的含「特殊量詞」(Distinctive Quantifier)(註7)或模糊量詞的三段論以及Philipps (1999)研究的「似然三段論」(Approximate Syllogism)等。
在這些學者中,Reichenbach (1952)、Thompson (1986)、Peterson (2000)和高東平(2006)都推廣了傳統的「周延性」概念,提出新的三段論有效性判斷規則。舉例說,根據Thompson (1986),以下三段論是有效的:
| 前提1: | Almost 50% of M are P. |
| 前提2: | Almost 55% of M are S. |
| 結論: | Some S are P. |
請注意上述推理不能歸結為單調性推理。
Philipps (1999)在「似然三段論」的研究方面提出了一些獨到的思想。他認為在研究某一推理模式時,不應只用簡單二分法把它分為有效或者無效,而應研究這個推理模式在甚麼情況下會較為可靠或較不可靠。試考慮以下這個推理模式:
| 前提1: | Q1 S are M. |
| 前提2: | Q2 M are P. |
| 結論: | Q3 S are P. |
古典邏輯只說,如果Q1 = Q2 = "some",不可能得到任何結論。Philipps (1999)則指出,當Q1和Q2的語義越強,同時Q3的語義越弱(例如"almost all"、"most"是語義強的量詞,"some"則是語義弱的量詞)時,上述推理模式便越可靠。此外,Philipps (1999)還指出,S與M這兩個集合的相對大小和元素分佈情況也會影響上述推理模式的可靠性。總括而言,Philipps (1999)提出了很多新思想,值得學者繼續深入研究。
第二個研究方向是把古典三段論與現代數理邏輯相結合,建構三段論的現代推理系統,這一方面的研究包括Ben-Avi and Francez (2005)的「自然演繹系統」以及由Third (2006)、Moss (2007, 2008a, b)、
Pratt-Hartmann (2004, 2009)、Pratt-Hartmann and Moss (2009)等建構的多個「公理系統」(註8)。雖然這些研究全都只集中於某一「片段」(Fragment)的三段論推理,但這些「片段」擴充了古典三段論的內容,屬於「新三段論」的範圍,Third、Moss和Pratt-Hartmann研究過的「新三段論」便有:含否定詞的三段論、含專有名詞的三段論、含一般動詞的三段論(古典三段論只使用系詞"be")、含並列結構的三段論、「關係三段論」(Relational Syllogism)(即前提和結論中包含多個量詞的三段論)等等。
舉例說,Moss (2008a)提出了一個只包含量詞"all"和"some"的三段論片段,這個片段有以下五條公理:
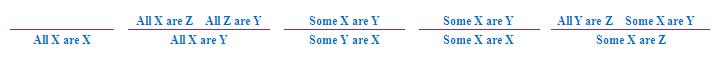
在上圖所示的每條公理中,紫色橫線上下的命題分別代表前提和結論,其中第一條公理沒有前提,因為"All X are X"是恆真的「重言式」。以下是利用上述公理進行推導的「證明樹」例子:
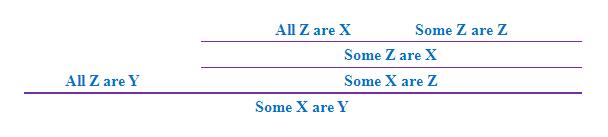
上述學者除了發掘「新三段論」外,更關注其推理系統的「元邏輯性質」(Metalogical Property)、「計算複雜性」(Computational Complexity)和「表達力」等問題,這些研究成果往往可以跟「人工智能」中的自然語言推理研究接軌,因此在現代邏輯研究中有重要價值。
第三個研究方向是借助各種數學工具建構全新的三段論,這些數學工具包括概率論、模糊數學和代數方法。
使用概率論方法的研究主要包括Dubois et al (1990, 1993)和Khayata, Pacholczyk and Garcia (2002)基於經典「條件概率」(Conditional Probability)以及Oaksford and Chater (2007)基於「貝葉斯概率」(Bayesian Probability)的研究。前者把量化句Q(A)(B)的真值條件看成以下關係:
其中Prob(B | A)代表給定x屬於A的條件下,x同時屬於B的條件概率,而Q則被看成概率值集合。為把研究結果應用於自然語言推理,上述學者嘗試用各種方法把數值計算結果轉換為自然語言的量詞,或嘗試建構一種「性質推理」(Qualitative Reasoning),即表面上直接以自然語言中的模糊量詞進行的推理(但背後仍須依賴數值計算)。
Oaksford and Chater (2007)則從心理學角度出發,認為一般人的推理模式不是基於經典邏輯的必然推理,而是基於「主觀概率」(即「貝葉斯概率」)判斷的似然推理。他們提出「概率法則模型」(Probability Heuristics Model)作為一般人進行三段論推理時的心理依據,而這個模型包含人們對概率、信息量和世界知識的判斷,因此儘管其推論不是必然的,但卻仍是符合理性的。Oaksford and Chater (2007)認為他們的理論能更真實反映一般人在日常生活中的推理。
使用模糊數學方法的研究主要包括Zadeh (1983, 1985)和Yager (1985a, b)的研究,特別值得一提的是Zadeh (1983, 1985)提出的「量詞擴張原理」(Quantifier Extension Principle)。設有以下三段論模式(寫成Q(x)的形式,其中Q代表量詞,x代表「參項」Parameter (註9)):
| 前提1: | Q1(x1) |
| 前提2: | Q2(x2) |
| 結論: | Q3(x3) |
「量詞擴張原理」是說,如果R(x1, x2, x3),則R(Q1, Q2, Q3),其中R代表某種函數/數值比較關係。換句話說,若參項之間存在某種函數/數值比較關係,則量詞之間也存在該種關係。我們可以利用這個原理來求出以下三段論中的Q3:
| 前提1: | (slightly more than half of)(|A ∩ B| / |A|) |
| 前提2: | (slightly less than half of)(|A ∩ B ∩ C| / |A ∩ B|) |
| 結論: | Q3(|A ∩ B ∩ C| / |A|) |
由於|A ∩ B ∩ C| / |A| = (|A ∩ B| / |A|) × (|A ∩ B ∩ C| / |A ∩ B|),根據「量詞擴張原理」,應有Q3 = (slightly more than half of) × (slightly less than half of),由此根據直觀,可知Q3大致上等於"(about a quarter of)" (註10)。
這裡的代數方法是指初等代數中的方法,這方面的研究計有Sommers (1970)、Murphree (1998)和Sommers and Englebretsen (2000)的「詞項函子邏輯」(Term Functor Logic),Murphree (1991, 1997)的「數值例外邏輯」(Numerically Exceptive Logic)以及沈小豐、喻蘭、沈鈺(2008)基於「邏輯代數」(Algebra of Logic)發展而來的「解析邏輯」(Analytical Logic)等。
「詞項函子邏輯」的特色是把邏輯推理轉化為正負項加減運算。Sommers (1970)和Sommers and Englebretsen (2000)把含"some"的主語和肯定性謂語表示為正項,把含"every"的主語和否定性謂語表示為負項,而有效三段論的一個必要條件是結論等於兩個前提之和(此外還須滿足其他條件)。舉例說,前述的"Barbara"三段論便可以表達為
| 前提1: | − M + P |
| 前提2: | − S + M |
| 結論: | − S + P |
請注意− S + P剛好等於(− M + P) + (− S + M),所以上述推理滿足前述必要條件。除了古典三段論外,Sommers and Englebretsen (2000)還研究了較少人問津的「關係三段論」,Murphree (1998)則把Sommers (1970)的理論擴展至包含數值比較量詞的量化句。
不過,Murphree對三段論推理的最大貢獻在於他所創立的「數值例外邏輯」,他把古典量化句推廣為含例外量詞的量化句,這些量化句各有四個等價形式,例如"Every S is P"便被推廣為以下四個等價命題:"At least all but x S are P"、"At most none but x S are non-P"、"At most none but x non-P are S"和"At least all but x non-P are non-S",並表達為下圖:
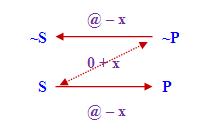
在上圖中,實線和虛線箭頭分別代表"at least ..."和"at most ...","@ − x"和"0 + x"則分別代表"all but x"和"none but x",其中x為整數。請注意當以0代入上圖中的x後,便可得到"Every S is P"。
Murphree (1991)還利用圖示法提出有效三段論的一個必要條件:把代表兩個前提的圖並排放在一起時,必須有有一個實線箭頭從S連至M和另一個箭頭從M連至P,其中第二個箭頭上的數式必須為"@ − x"的形式。舉例說,我們可以驗證前述"Barbara"三段論的有效性如下,先把兩個前提和結論表達為下圖:
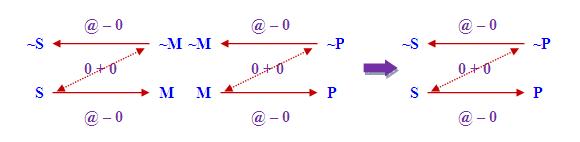
在上圖中,我們可以從最左的S沿實線箭頭走到M,然後從M沿另一個實線箭頭走到P,而且第二個箭頭上的數式為"@ − 0",符合前述規定。請注意由於有M的中介作用,在兩個前提中本來沒有連繫的S和P,在結論中被連貫起來了。
筆者認為,Murphree (1991)理論的最大價值在於可以與前述的「量詞擴張原理」融合。舉例說,利用Murphree (1991)的圖示法,我們可以把"Barbara"三段論重新表述為以下的Q(x)形式:
| 前提1: | (at most 0)(|M − P|) |
| 前提2: | (at most 0)(|S − M|) |
| 結論: | (at most 0)(|S − P|) |
容易證明|S − P| ≤ |M − P| + |S − M|,由此根據「量詞擴張原理」,應有(at most 0) ≤ (at most 0) + (at most 0),容易看到這個不等式是真的。由此可見,「量詞擴張原理」不僅是模糊三段論的必要條件,也是普通三段論的必要條件,因此筆者認為,「量詞擴張原理」是一切三段論背後的普遍原理之一。有關三段論推理的其他內容,請參閱拙文《廣義量詞系列:古典推理模式》和《廣義量詞系列:三段論推理的革新》。
在古典邏輯中,「對當推理」(Opposition Inference)是指以「對當關係」(Opposition Relation)為基礎的推理,而「對當關係」則是指包含四個經典量詞(即"every"、"no"、"some"和"not every")的量化句(分別記作A、E、I和O)之間的各種邏輯關係,其定義見下表(在以下定義中,設p和q為量化句):
| 名稱 | 定義 |
|---|---|
古典邏輯學家把四個量化句和以上關係排成以下方陣,稱為「對當方陣」(Square of Opposition)(請注意在以下方陣中,「所有S不是P」等價於「沒有S是P」;「有S不是P」等價於「並非所有S是P」):
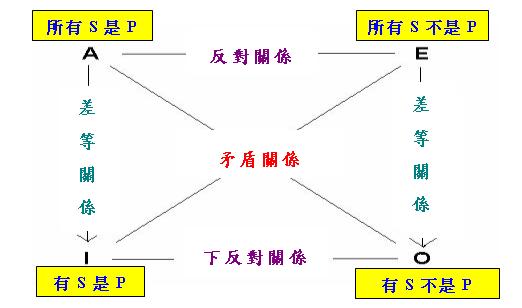
在古典邏輯中,「對當推理」的重要性僅次於「三段論推理」,雖然在數理邏輯興起後其地位已大不如前,但在當代它又重新引起部分學者的研究興趣,2007年世界各地學者更舉行了「第一屆對當方陣世界大會」,足見其在現代自然邏輯中的重要性。當代學者對「對當推理」的研究可粗略地分為三個方向,現分述於下。
第一個研究方向是探尋對當方陣背後的原理,從而發掘出新的對當方陣,或把對當方陣應用於更廣闊的層面,這方面的研究包括以下內容:de Laguna (1912)發現對當方陣與三段論推理之間存在密切聯繫;Brown (1984)根據主、謂語之間的各種真假關係而劃分出四大類(下分34小類)對當方陣;繆四平(1994)提出含關係命題的對當方陣;黃士平(1998)把對當方陣拆解為「對角關係」與「周邊關係」之間的互動;Jaspers (2005)以平面直角坐標系表述對當方陣;Seuren (2007)提出「改良對當方陣」以及周家發(2006)提出「對當方陣一般模式」(General Pattern of Squares of Opposition)等。
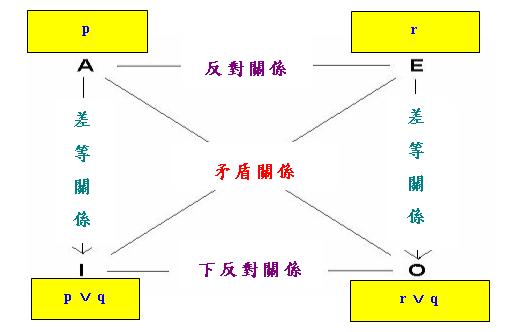
「對當方陣一般模式」有兩個等價形式,其第一形式是說:設有命題p、q、r滿足「三分關係」(Trichotomy),即這三個命題兩兩互斥且合起來窮盡一切可能性,那麼我們可以構造以下對當方陣:
第二形式則是說,設有命題s和t滿足「單向蘊涵關係」,即s蘊涵t,但t不蘊涵s,那麼我們可以構造以下對當方陣:
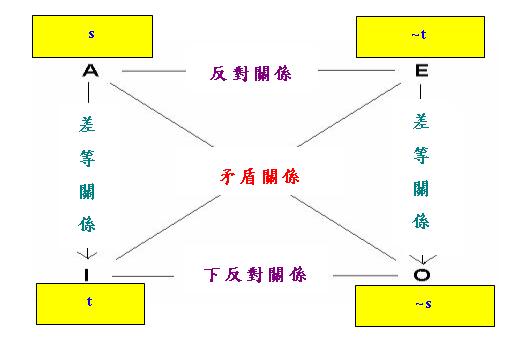
利用上述兩個形式,便可以構造出無限多個以往邏輯學家沒有發現的對當方陣。
第二個研究方向是構造各種對當圖形。早在1950年代,Reichenbach (1952)和Blanche (1953)便分別提出「對當立方體」和「對當六角陣」,其中「對當六角陣」是在古典邏輯的四個量詞之上加上兩個「特殊量詞」-"some but not all"和"all or no"後所得的圖形(包含這兩個量詞的量化句分別記作Y和U)。此後,Beziau (2003)和Horn (2007)分別從邏輯學和語言學角度繼續深入探討「對當六角陣」;而其他學者則提出各種對當圖形,包括周訓偉 (2006)的「邏輯矩形」和「邏輯餅」、Seuren (2007)的「對當八角陣」和「對當十二角陣」、Wolenski (2008)的「對當八角陣」、Moretti (2004)的「對當十四面體」等,Moretti (2004)更發展出一套聯繫邏輯學與幾何學的「n對當理論」(n-Opposition Theory)。以上所述的圖形要麼是對「對當方陣/六角陣」的重新解釋,要麼是加入「模態算子」的結果,後者已超出本文討論的範圍。
Moretti (2004)指出,對於滿足「三分關係」的命題p、q和r來說,能最圓滿地表達這個「三分關係」的圖形不是「對當方陣」,而是「對當六角陣」,這是因為這三個命題加上它們的析取,合共有六個「非平凡」命題:p、q、r、p ∨ q、q ∨ r、p ∨ r,剛可構成一個「對當六角陣」(註11),如下圖所示(下圖沒有標出各個「差等關係」的箭頭方向,讀者應不難補出):
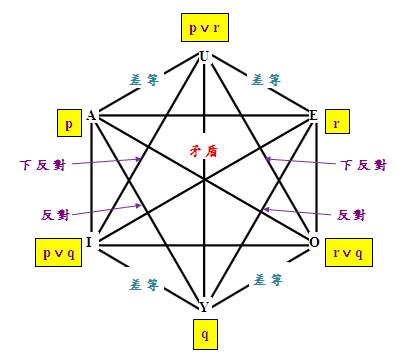
上圖的六個命題之間共有15個關係,但為免使上圖過於複雜,這裡略去了傳統「AEOI對當方陣」上的六個關係。細看之下,上圖其實還包含著另兩個「對當方陣」:AUOY和UEYI;此外還有一個「AYE反對三角陣」和一個「IOU下反對三角陣」。由此可見,傳統的「對當方陣」只是「對當六角陣」上的一個局部範圍。
筆者認為,我們可以把以上情況推廣至「n分關係」(n ≥ 3):設有滿足「n分關係」的n個命題p1 ... pn,即這n個命題兩兩互斥且合起來窮盡一切可能性,那麼我們可以構造以下
的「對當2n角陣」:
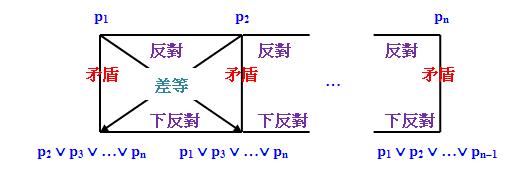
請注意上圖中尚有很多關係沒有繪出來,但不難看出,上圖中所有垂直線都代表「矛盾關係」,上排任意兩個命題之間具有「反對關係」,下排任意兩個命題之間具有「下反對關係」,上排任一命題與不在其垂直線的下排任一命題之間具有「差等關係」。
第三個研究方向是把對當關係加以推廣或精細化。傳統的對當方陣依賴於一個「主語存在預設」,即A和E句的主語S所指的事物必須存在,否則除了「矛盾關係」外,對當方陣上的其他關係都不成立。Reichenbach (1952)把否定詞"~"加入量化句中,由此產生了其他預設問題。為了區分不同的預設,Reichenbach (1952)把「矛盾關係」以外的對當關係各細分為幾個次類,這些次類可稱為「精細化對當關係」(Refined Opposition Relation)。Reichenbach (1952)正是利用這些「精細化對當關係」構造他的「對當立方體」。
舉例說,「差等關係」可分為三個次類:「真差等關係」(Proper Subalternation),即傳統的「差等關係」,須依賴於「主語存在預設」,即S ≠ Φ;「斜差等關係」(Slant Subalternation)須依賴於預設S ≠ P;「交差等關係」(Cross Subalternation)則須依賴於預設P ≠ U (其中U代表論域)。容易驗證,"Every S is P"與"Some ~S is P"存在「斜差等關係」,而"Every S is P"與"Some ~S is ~P"則存在「交差等關係」。例如若S = P,則"Every S is P"真而"Some ~S is P"卻假;而在其他情況下,則有Every S is P ⇒ Some ~S is P。
除了從預設角度分解出對當關係的次類外,我們也可以從集合關係的角度推廣對當關係,即把對當關係看成集合之間的關係(註12)。根據集合論,兩個集合X與Y之間有以下五種「標準集合關係」:「重合關係」、「真子集關係」、「真母集關係」、「不相交關係」和「交錯關係」,下圖顯示這五種「標準集合關係」的定義及名稱:
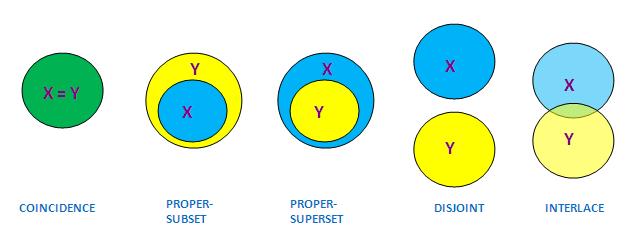
從上圖可見,「差等關係」可以被看成COINCIDENCE和PROPER-SUBSET的「并」,即X對Y存在「差等關係」當且僅當X與Y重合或X是Y的真子集。
不過,「標準集合關係」還不是最基本的,這是因為這五種關係沒有考慮X或Y與論域U的關係,因而無法區分「矛盾關係」與「反對關係」。如果我們把U加入上圖,將可得到更細致的分類。根據Brown (1984),兩個集合之間共有15種「基本集合關係」,下圖顯示這15種「基本集合關係」的定義及名稱(下圖中如不出現X或Y,則代表X或Y等於空集):
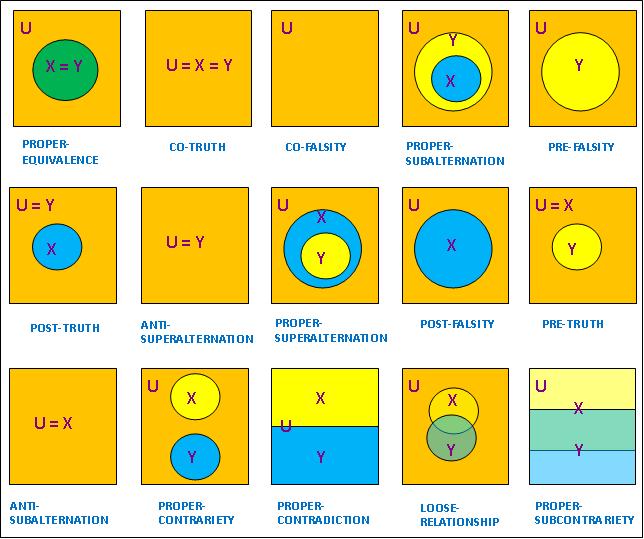
請注意前述五種「標準集合關係」中的每一種都可被看成某些「基本集合關係」的「并」,例如COINCIDENCE便等於EQUIVALENCE、CO-TRUTH和CO-FALSITY的「并」。
上圖顯示,各種古典對當關係可被看成某些「基本集合關係」的「并」,例如「差等關係」便等於EQUIVALENCE、CO-TRUTH、CO-FALSITY、PROPER-SUBALTERNATION、PRE-FALFSITY、POST-TRUTH和ANTI-SUPERALTERNATION的「并」。此外,古典對當方陣遺漏了一些關係,例如PROPER-SUPERALTERNATION等。
由此可見,如果我們把上述「基本集合關係」加以組合,將可得到各種「廣義對當關係」(Generalized Opposition Relation)。「廣義對當關係」的提出可以彌補古典對當關係的不足。前面說過,給定滿足「n分關係」的n個命題p1 ... pn,我們可以構造「對當2n角陣」,但這個圖形並未涵蓋所有可能析取命題,例如p1 ∨ p4和p2 ∨ p4 (設n = 4)便不在這個圖形之上,這是因為古典對當關係未能概括這些析取命題之間的關係。但在引入「廣義對當關係」後,這個問題便不復存在,這是因為任何兩個析取命題之間都有一種「廣義對當關係」成立,例如前述兩個析取命題之間的關係便是LOOSE-RELATIONSHIP。
由此我們可以把「對當2n角陣」作進一步推廣:設有滿足「n分關係」的n個命題p1 ... pn以及一組兩兩互斥且窮盡一切可能性的「廣義對當關係」,那麼我們可以這組「廣義對當關係」為基礎構造一個「對當2n角陣」。下圖顯示以15種「基本集合關係」為基礎的「對當24角陣」的部分內容:
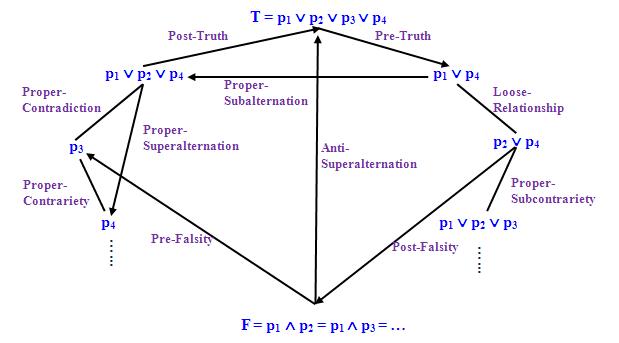
請注意「對當2n角陣」應是最詳盡表達「n分關係」的圖形。
根據廣義量詞理論的觀點,量化句"Q S is P"中的量詞Q表達集合S與P之間的關係,現在如果我們把前述的「廣義對當關係」套用於Q,將可得到很多新的量詞,所得的量化句稱為「廣義直言命題」(Generalized Categorical Statement)(註13),田龍九(1981)和黃衛星(1994)便是循此方向分別總結出14和25種有研究價值的「廣義直言命題」,例如田龍九(1981)提出的命題「只有一些S是P」便代表S對P存在「真母集關係」(即PROPER-SUPERSET)。
於此順帶一提「謂語量化」(Quantification of the Predicate)的問題。在一般直言命題中,量詞只出現於主語。但在19世紀中葉,Hamilton提出一種主、謂語皆包含量詞的量化句,例如"Every S is every P"、"Some S is every P"等,以下稱為「謂語量化句」。由於這類量化句的語義難以理解,沒有引起學界共鳴。及至一個世紀多後,Fogelin (1976)根據「周延性」定義解釋「謂語量化句」的語義,重新引起學界對這類量化句的注意。根據Fogelin (1976),所有「謂語量化句」都等價於某種普通量化句,例如
從「廣義對當關係」的角度看,以上兩句分別表達S與P之間的「重合關係」以及S對P的「母集關係」(即COINCIDENCE與PROPER-SUPERSET的「并」)。由此可見,「謂語量化句」在本質上是一種「廣義直言命題」。
根據量詞和對當關係的定義,我們可以得到某些有效推理,例如根據"every"與"no"的「反對關係」,我們有
不過,上述推理似乎過於直觀平凡,因此筆者在這裡提出一些構想,冀能建構一種「對當演算」(Opposition Calculus),藉以發掘一些較有趣的推理模式。現時在這方面尚未形成一種研究方向,只有一些零星的研究,其中值得一提的是MacCartney (2009)的「自然語言推理」模型。該模型由多個模塊組成,其中一個模塊專門進行以下這種「對當三段論」推理:
此外,van Benthem (2008)也曾提過一種由「單調性演算」推廣而來的推理,以下把他的構想表述為更一般的形式。首先,我們可以把「左遞增性」推理的定義表述為:
現在,如果我們把上式中的"⊆"改為一般的「廣義對當關係」(記作GOR),便可得到「左對當演算」的一般定義如下:
其中GOR(A, A')代表A和A'具有GOR這種「廣義對當關係」。舉例說,當GOR = DISJOINT時,Q = "only"滿足(14),而Q = "all"則不滿足(14)。具體例子為,已知"elderly"與"youngsters"存在DISJOINT關係,我們有"Only elderly are admitted"與"Only youngsters are admitted"也存在DISJOINT關係,但"All elderly are admitted"與"All youngsters are admitted"卻不存在DISJOINT關係。如何找出滿足(14)的量詞,還有待學者深入研究。有關對當推理的其他內容,請參閱拙文《廣義量詞系列:古典推理模式》和《廣義量詞系列:直接推理的革新》。
「論元結構推理」(Argument Structure Inference)泛指對量詞或其論元進行各種操作(包括各種布爾運算和易位等)而得的推理,這種推理對應於古典邏輯中的「結構變換推理」(亦稱「變形推理」)(Immediate Inference)。古典邏輯研究三種「結構變換」:「換質法」(Obversion)、「換位法」(Conversion)和「換質位法」(Contraposition)。由於「換質位法」是前兩種變換的結合,這裡只擬介紹前兩種變換。
「換質法」就是把量化句的量詞換質(即把"every"和"no"互換,或把"some"和"not every"互換),並同時把謂語變成其否定。進行「換質法」前後的量化句互相等價,例如
「換位法」則是把量化句的主語(不含量詞的部分)與謂語易位。當量詞是"some"或"no"時,進行「換位法」前後的量化句互相等價,例如
從以上定義可見,「結構變換推理」就是對量詞論元進行否定或易位而得的推理,可說是古典的「論元結構推理」。在本節筆者將介紹現代的「論元結構推理」,這種推理可分為兩小類:「對偶性推理」和「對稱性推理」,分別對應著古典的「換質法」和「換位法」,以下分節介紹。
「對偶性推理」(Duality Inference)是指對量詞或其論元進行否定而得的推理。「否定」是一個多層次的概念,當代學者提出了三種否定概念,現把這幾個概念的名稱和定義列於下表(註14):
| 名稱 | 定義 |
|---|---|
從以上定義可以看到,「右對偶」其實是「外部否定」和「右內部否定」的結合。根據上述定義,我們可以求出各種限定詞之間的否定關係。比如說,"some"與"no"互為「外部否定」,"no"與"every"互為「右內部否定」,"some"與"every"互為「右對偶」等。上述關係不難驗證,例如由於有以下等價關係:
可知"no"與"every"的確互為「右內部否定」。
當代一些學者,例如Gottschalk (1953)、Lobner (1983, 1987)、Englebretsen (1984)、Peters and Westerstahl (2006)等,使用這三個概念重新定義古典對當方陣,構造了以下的「對偶方陣」
(Square of Duality):
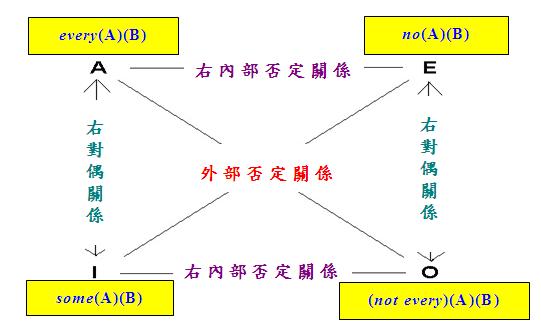
惟請注意,上述學者大多把他們研究的「對偶方陣」稱為「對當方陣」。可是,這兩種方陣是不相同的,兩者最大的差異在於,「右內部否定關係」是對稱的,而「差等關係」卻是不對稱的;而且兩者建立在不同的基礎上,因此之故,前述的「對當方陣一般模式」並不適用於「對偶方陣」。
對於包含左、右兩個論元的限定詞來說,「右內部否定」和「右對偶」只涉及右論元。因此我們可以把這兩個概念推廣為「左內部否定」和「左對偶」,乃至「左右內部否定」和「左右對偶」,分別用Q~l、Qld、Q~lr和Qlrd來表示。事實上,Gottschalk (1953)早在1950年代便已提出三種否定概念,其中兩種相當於「左右內部否定」和「左右對偶」;而de Mey (1990)則更明確提出上述四種否定概念。
提出更多否定概念後,我們便可以得到更多限定詞之間的否定關係,例如"only"與"no"互為「左內部否定」,"only"與"every"互為「左右內部否定」,"only"與"some"互為「左對偶」,"only"與"not every"互為「左右對偶」等。
利用上述定義,我們可以推導出一些有效推理模式,這些推理模式最初由Keenan (1993)和Zwarts (1996)提出,後來Keenan (2003, 2008)再將之系統化。一言以蔽之,「對偶性推理」的實質就是利用「雙重否定律」(即~~A ≡ A)的結果,例如以下推理模式:
利用前述的定義以及「雙重否定律」,容易證明上述模式是正確的。以下是應用(17)以及"only"與"every"互為「左右內部否定」的一個例子:
假如我們把(15)中的Q換成Q1,並且把B換成Q2(B)(V),便可得到一個包含兩重量詞的推理模式(註15):
在廣義量詞理論中,"Q1(A)[Q2(B)(V)]"被稱為「迭代量化句」,它代表自然語言中主語和賓語均帶有限定詞的句子,其中"Q1(A)"代表主語,"Q2(B)"代表賓語,"V"代表動詞,例如"Every boy loves some girl"便可表達為(請注意在下式中,LOVE處於兩個限定詞的轄域內,所以被置於最後):
利用(18),以及"every"與"no"互為「右內部否定」和"some"與"no"互為「外部否定」此一事實,我們可以得到以下「迭代量化句」推理:
在(18)中,代表動詞的B也可成為否定的對象,此即Zwarts (1996)所提出的「動詞否定」(Verb Negation),在此情況下,我們要把(18)改為
請注意(19)同時包含「右內部否定」、「右對偶」和「外部否定」這三種操作。以下是利用(19)的一個廣州話推理實例:
請注意在以上例子中,「個個學期」與「冇一個學期」互為「右內部否定」,「至少一堂」與「堂堂」互為「右對偶」,「唔上」與「上」互為「外部否定」(亦即「矛盾概念」)。
我們還可以對(19)作進一步推廣。如果我們把(19)中的V換成Q3(C)(V),便可得到一個包含三重量詞的推理模式。由於這個模式頗為複雜,這裡不擬作詳細討論。
「不動點」(Fixed Point)與「自對偶」(Self-Dual)本來是數學上的概念,廣義量詞理論借用過來指稱具有某些特性的量詞。這兩個概念其實是同一個概念,是指那些等價於其「內部否定」或「對偶」的量詞。舉例說,「右內部否定不動點」和「右自對偶」的定義分別如下:對任意A、B,均有
Keenan (2003, 2008)和Zuber (2005)提出了自然語言量詞中的多個「不動點」和「自對偶」,例如"exactly half of"和"some but not all"是「右內部否定不動點」,而專有名詞、反身代名詞和"more than 3 of the 7"則是「右自對偶」等。由此根據定義(20)和(21),並結合上一小節的推理模式,我們有以下有效推理:
Keenan (2003, 2008)等人只研究了右論元上的「不動點」和「自對偶」,筆者認為可以把他們的研究成果推廣至左論元乃至左右論元(惟請注意,自然語言中不存在「外部否定不動點」和「左右自對偶」),例如不難證明,"some but not restricted to"是「左內部否定不動點」,"all and only"是「左右內部否定不動點」等。由此結合上一小節的推理模式,我們有以下有效推理:
「否定」和「對偶」概念具有普適性,因此其應用不限於廣義量詞,而可以推廣至其他層面。de Mey (1990)便把「命題聯結詞」(例如"if"、"or"等)看成「真值限定詞」,以下便是"if"的真值條件(在以下定義中,p和q代表命題):
這樣我們便可以把各種「否定」概念推廣至「命題聯結詞」,並推知"if"與"or"互為「左內部否定」等。由此還可以得到一些有效推理模式,例如根據前面的(16),我們有
上式也就是命題邏輯中對"if"的定義。
Lobner (1983, 1987)則提出「階段量」(Phase Quantification)的概念,並把某些「體貌副詞」(Aspectual Adverb)(例如"still"、"not yet"等)和「體貌動詞」(Aspectual Verb)(例如"begin"、"stop"等)看成「階段量詞」,並把各種「否定」概念推廣至這些詞項,例如"still"與"not yet"互為「內部否定」,"begin"與"stop"也互為「內部否定」等。由此可以得到一些有效推理,例如(以下假設"asleep"與"awake"以及"be silent"與"make noise"互為「外部否定」):
有關對偶性推理的其他內容,請參閱拙文《廣義量詞系列:對偶性推理基礎》和《廣義量詞系列:對偶性推理進階》。
「對稱性推理」(Symmetry Inference)是指對量詞或其論元進行易位而得的推理,對於只包含一個限定詞的量化句來說,易位只可能發生於該兩個論元之間,其推理模式為:
自然語言中有很多限定詞滿足上述模式,例如"some"、"no"、"exactly n"、"no ... except John"等,由此可得到以下有效推理:
對於限定詞而言,「對稱性推理」只有(22)這種模式,似乎貧乏了一點。但筆者認為可以把(22)推廣為
以下把這種推理稱為「逆向性推理」(Converse Inference),因為在上式中,Q1與Q2的關係類似「詞匯語義學」(Lexical Semantics)中研究的「逆向反義詞」(舉例說,"parent"與"child"、"send a letter to"與"receive a letter from"以及動詞的「主動態」與其「被動態」便各為「逆向反義詞」,例如"x loves y" ⇔ "y is loved by x")。
在自然語言中,滿足(23)的限定詞不多,"every"與"only"是其中一對,另一對則是較少人察覺的"all ... except John"與"apart from John only",以下是後者的一個例句:
請注意以上兩句都表示:John是不穿制服的會員,而其他會員都穿制服。
對於包含兩個限定詞的「迭代量化句」來說,易位可以發生於該兩個限定詞之間。由此我們有以下推理模式:
在上式中,Vc代表動詞V的「逆向反義詞」。我們把(24)所定義的性質稱為「轄域獨立性」(Scope Independence)。當Q1(A) = Q2(B)時,我們把這種性質稱為「自交換性」(Self-Commutativity)。如果Q1(A)是固定的,而Q2(B)是可變的,我們便把這種性質稱為「無轄域性」(Scopelessness)。Zimmermann (1993)和Westerstahl (1996)研究了上述三種性質,發現專有名詞是「無轄域」的;專有名詞以及"every A"、"some A"等是「自交換」的;而任意兩個專有名詞以及"every A"與"every B"、"some A"與"some B"之間則是「轄域獨立」的。由此可以得到一些有效推理,例如根據"every boy"與"every girl"的「轄域獨立性」,有
如果我們把(24)中的"⇔"改為"⇒",所得關係稱為「轄域支配」(Scope Dominance)。具體地說,Q1(A)轄域支配Q2(B)當且僅當
Ben-Avi and Winter (2004)、Altman, Peterzil and Winter (2005)以及Altman and Winter (2005)對這個課題進行了深入研究,總結出一系列有關「轄域支配」的定理。舉例說,他們發現"most A"轄域支配"no B",由此可以得到以下有效推理:
如果我們對限定詞的論元同時進行內部否定和易位,將可得到「逆否性推理」(Contrapositivity Inference),其具體推理模式為
Zuber (2006)研究了「逆否限定詞」與「對稱限定詞」的關係,發現Q是「逆否」的當且僅當Q~r是「對稱」的,由此可知"every"、"not every"、"all except n"、"all ... except John"等都是「逆否」的。此外,他還發現Q是「逆否」的當且僅當其「逆向反義詞」是「逆否」的,由此又可知"only"、"not only"、"apart from John only"等也是「逆否」的。把這些限定詞代入(26),便可得到一些有效推理,例如
從更廣的角度看,「對稱性」和「逆否性」只是限定詞眾多「代數性質」和「關係性質」中的兩種,而限定詞的這些性質的定義一般表達為蘊涵式或等值式,可以被看成某種推理模式,例如限定詞的一種重要性質-「右守恆性」(Right Conservativity)便是由以下等值式定義:
有些性質的定義涉及三個量化句,更像三段論推理,例如「循環性」(Circularity)的定義為
Zwarts (1983)、van Benthem (1984)、Westerstahl (1984)、Zuber (2005, 2006)等對這些性質進行了深入研究,找出滿足各種性質的限定詞。他們的研究成果讓我們得到更多有效推理模式,例如由於"every"滿足(27),我們有以下推理:
他們發現的某些否定性成果也讓我們知道某些推理模式是不可滿足的,例如(28)就是一種不可滿足的推理模式(至少就滿足「右守恆性」的限定詞而言)。
此外,當前「形態學」(Morphology)和「句法學」(Syntax)的研究(例如Haspelmath and Muller-Bardey (2004)和Han (2007))還揭示了對論元結構的其他操作,這些操作往往可以表述為推理模式,例如英語中用"make"生成的「使役化」(Causativization)句子與其原句之間便存在蘊涵關係,例如
不過,這些操作跟量化句並無直接聯繫,已超出本文的討論範圍。有關對稱性推理及其擴展的其他內容,請參閱拙文《廣義量詞系列:直接推理的革新》、《廣義量詞系列:量詞的代數性質》、《廣義量詞系列:量詞的關係性質》和《轄域歧義》。
至此筆者已介紹了有關廣義量詞四大類自然邏輯推理的各種理論框架,其中以「廣義量詞理論」(Generalized Quantifier Theory)和「範疇語法」(Categorial Grammar)最為重要。「廣義量詞理論」的特點是以集合論語言表述廣義量詞的真值條件,例如把"every(A)(B)"的真值條件表述為A ⊆ B。「範疇語法」(註16)的特點則是把句子的生成過程表述為句中各個「範疇」(「範疇語法」把句子和各種詞類統稱為「範疇」)之間的推導關係,這種推導關係類似邏輯推理。
舉例說,如果把句子、名詞短語和不及物動詞短語分別簡記為s、np和np → s (不及物動詞短語的特點是,當它與一個名詞短語結合後,便成為一個句子,所以記作np → s),那麼"Mary danced"的生成過程便可以表述為

請注意上圖中的推導類似命題邏輯中「肯定前件律」(Modus Ponens)的運用,即給定p和p ⇒ q,可以推出q。
除了以上兩種理論外,當今尚有其他理論框架也可劃歸「自然邏輯」的範圍,但由於它們的研究內容不屬於上述四大類推理,所以留待本節才作出介紹。
以Montague (1973)為代表的「蒙太格語法」(Montague Grammar)一般被視為當代「形式語義學」(Formal Semantics)的開端,其最大貢獻是把一階謂詞邏輯成功應用於自然語言的語義分析中,打破了人工邏輯語言與自然語言之間的藩籬。雖然Montague (1973)是以一階謂詞邏輯來表述自然語言句子,但他借用當代邏輯的「λ演算」(λ-Calculus)理論使其表達式能反映自然語言句子的句法結構。舉例說,在一階謂詞邏輯下,
一般表達為
上式沒有反映(29)的句法結構;但在「蒙太格語法」下,(29)卻可表達為
其中"λPλQ∀x(P(x) ⇒ Q(x))"便是"every"的表達式,請注意(31)比(30)較貼近(29)的句法結構。後來「廣義量詞理論」索性用廣義量詞"every"代替這個表達式,使(31)在形式上更貼近(29)。
可是,Montague (1973)沒有處理自然語言邏輯推理的問題,這方面的工作乃由McAllester and Givan (1992)完成。McAllester and Givan (1992)採用在形式上比Montague (1973)更貼近自然語言的表達式,例如把句子"Every child of a bird is a friend of every bird watcher"表達為
他們的理論框架可以證明某些「關係命題」推理,例如
不過,他們是從人工智能自動推理的角度研究自然語言推理問題,所以較關注「可判定性」和「計算複雜性」等理論問題。為易於處理這些理論問題,他們的理論框架只包括古典邏輯中的四個量詞,其表達力甚為有限。
由Keenan and Faltz (1985)開創的「布爾語義學」(Boolean Semantics)是一種結合「布爾代數」(Boolean Algebra)與「形式語義學」的理論。「布爾語義學」把自然語言中的各種詞類和語言單位類別處理成「布爾代數」,即含有「并」(∨)、「交」(∧)、「補」(~)這三種運算以及「偏序關係」(≤)的集合(上述運算和關係須滿足某些公理),例如所有名詞短語構成一個「名詞短語代數」,所有句子又構成另一個「句子代數」。
這種理論把能夠出現於自然語言不同層面(詞、短語、分句)的"or"、"and"和"not"處理成同一種運算,例如"John or Mary"是「名詞短語代數」上「并」運算的結果,而"John sang or Mary danced"則是「句子代數」上「并」運算的結果。類似地,自然語言不同層面上的包含/蘊涵關係也可以處理成同一個「偏序關係」,例如在「名詞短語代數」中,"boys"與"human beings"之間的包含關係可以表達為
而在「句子代數」中,"John sang"與"John sang or Mary danced"之間的蘊涵關係也可以表達為
後來,Winter (2001)進一步發展「布爾語義學」,把這套理論應用於並列關係、複數名詞和轄域的語義解釋。
上述學者主要是借助「布爾語義學」來解釋某些語義問題而非邏輯推理。不過,Zuber (2002, 2003)以「布爾語義學」為基礎,提出了一種嶄新的推理關係-「跨類蘊涵」(Intecategorial Entailment)。如前所述,一般的包含/蘊涵關係都是同一個「布爾代數」內成員之間的關係,但Zuber (2002, 2003)指出,不同「布爾代數」的成員之間也可以存在蘊涵關係,例如
上式表達「名詞短語代數」與「句子代數」之間的「跨類蘊涵關係」,其中下標"IC"代表「跨類」(Intercategorial)。上式之所以成立,是因為不論名詞短語"the mosquito net that Leo bought"出現於任何合語法句子的任何部分,該句都必蘊涵"Leo bought a mosquito net"。
請注意(32)其實也可看成語用學中研究的「預設」(Presupposition)關係,即"the mosquito net that Leo bought"預設"Leo bought a mosquito net"。雖然並非所有「跨類蘊涵關係」都屬於「預設」關係,但「跨類蘊涵」概念的提出的確為「預設」(以及其他語言現象)的研究提供了一個全新視角。
「計算語義學」(Computational Semantics)是一個嶄新的學科,專門研究如何用電腦或程式語言實現邏輯學或形式語義學所作的語義分析成果,包括用電腦實現「自然語言推理」。「計算語義學」可以採用不同的研究方式,有些學者把自然語言句子翻譯成一階謂詞邏輯表達式,然後進行處理,例如Blackburn and Bos (2005);有些學者則採用自然邏輯的模式,在自然語言句子上加上各種標記,然後進行處理,此即「文本推理」(Textual Inference)。較有代表性的「文本推理」研究包括Nairn, Condoravdi and Karttunen (2006)以及MacCartney and Manning (2007),請注意前述MacCartney (2009)的「自然語言推理」模型就是結合這兩種「文本推理」的成果,其中MacCartney and Manning (2007)主要研究「單調性演算」和「對當演算」,這在前面已作介紹,以下介紹Nairn, Condoravdi and Karttunen (2006)的研究內容。
Nairn, Condoravdi and Karttunen (2006)研究某些可帶(限定或非限定)從句的動詞的推理問題,舉例說,在句子
中,動詞"forgot"後帶非限定從句,上句分別蘊涵和預設(註17)以下第一和第二句:
有趣的是,當"forgot"後帶限定從句時,整句的預設跟前述截然不同,例如下面第一句預設第二句:
以往很多學者對上述情況作出了研究,Nairn, Condoravdi and Karttunen (2006)的工作就是把這些研究成果轉化為一種能由電腦執行的算法。由於電腦跟人腦有很大差異,「計算語義學」有很多該學科獨有的課題,這方面的研究可說是方興未艾,還有大量工作要做。
「非標準邏輯」(Nonstandard Logic)是指古典邏輯和數理邏輯以外的邏輯,在當代興起了大批「非標準邏輯」,本文無法介紹哪怕一小部分,因此這裡只擬介紹兩個可歸入「自然邏輯」範疇的推理系統,即Suppes (1979, 1981)和Purdy (1991, 1992)的系統。
Suppes (1979, 1981)受當時風行的「轉換生成語法」(Transformational Generative Grammar)的影響,因此他在其設計的邏輯系統中,定出一些生成英語句子的句法規則以及相應的語義表達式,例如以下是其中一條規則及其表達式(略作簡化):
其中"S"、"EQ"、"NP"和"VP"分別代表「句子」、「存在量詞」、「名詞短語」和「動詞短語」,[NP]代表由"NP"所指個體組成的集合等。Suppes (1979, 1981)基於這些規則和表達式,提出一些推理規則,例如其中一條規則是
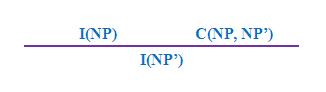
其中I(NP)代表以「存在量詞 + NP」為主語的句子,C(NP, NP')則代表形如"All NP are NP' "的句子,或者NP = NP'加上一些修飾語。根據以上規則,我們有以下有效推理:

以上推理符合上述規則,其中"black"是形容詞,是作為"cows"的修飾語。
請注意Suppes (1979, 1981)力圖直接從英語的表層句法結構進行推理,所以他把推理規則定得非常細致具體;但由於自然語言句法結構靈活多變,同一個句法單位可能出現於不同位置,這樣Suppes便要為每一種句法單位可能出現的每一個位置設立一條句法規則,使他的規則變得非常繁瑣和缺乏概括性。
Purdy (1991, 1992)則力圖建構一種類似三段論但比三段論涵蓋面廣的「表層語言推理」(Surface Reasoning)系統,他所指的「表層語言」是以「包含」(Inclusion)、「排除」(Exclusion)和「相交」(Overlap)這三種最基本邏輯關係為基礎的語言,而這三種關係正是分別由自然語言中最常用的三個限定詞"all"、"no"和"some"來表達,因此他認為他的系統能較佳地反映人類的推理機制。
表面上看,Purdy (1991, 1992)的邏輯系統跟一階謂詞邏輯很相似,因為他的系統也包含公理和推理規則,他也為其系統設計了搜尋證明的策略(當今的數理邏輯也有各種搜尋證明的方法,例如「歸結法」Resolution Method、「表列法」Tableau Method等)。但Purdy (1991, 1992)強調他的系統跟古典三段論一樣,是以「類別」(Class,即相當於「集合」)為基礎,因此他的語義表達式跟同樣以集合論為基礎的廣義量詞理論表達式頗為相似,例如他把"Some horses are faster than some dogs"表達為
Purdy (1991, 1992)亦強調,他的系統較古典三段論涵蓋面廣,可以推導出古典三段論沒有研究的「關係三段論」,例如他便示範了如何用他的系統證明以下三段論:
| 前提1: | Some horses are faster than some dogs. |
| 前提2: | All dogs are faster than some men |
| 結論: | Some horses are faster than some men. |
本文介紹了「自然邏輯」的各種理論,其實從更廣的角度看,當今尚有多種從語言學、邏輯學、數學、語言哲學乃至心理學角度研究自然語言推理的理論,由於這些理論並不都屬於「自然邏輯」的範圍,而且筆者所知有限,本文不能一一介紹。但筆者相信,透過本文的介紹,讀者應能了解,自然語言推理有非常豐富的內容,本文介紹的推理只涵蓋了一小部分,自然語言推理尚有其他類型以及很多未被發現的奧秘,有待我們深入挖掘。
註1:有關本節所提學者的理論的詳細內容,將留待下文再述。

