筆者在《廣義量詞系列:對偶性推理基礎》中介紹了當代「對偶性推理」的基本原理。「對偶性推理」作為一種只有很短歷史的推理模式,本身沒有很豐富的內容,但經Keenan、Westerstahl、Zuber等人的深入研究後,已發掘出很多新的內容。本文將主要介紹上述學者對此一課題的一些研究成果,並加上筆者的一些個人研究成果。
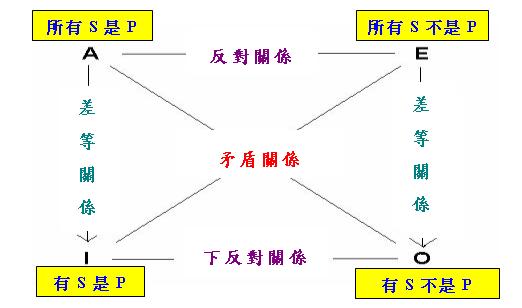
從某一角度看,上一章介紹的「外部否定」、「內部否定」和「對偶」概念是對傳統「對當關係推理」的一種改造。「對當關係推理」是「古典形式邏輯」所研究的量化句推理的一種,古代學者把這種推理總結為以下的「古典對當方陣」:

但正如筆者以往指出的,傳統「對當關係推理」中的「差等關係」之所以成立,其實依賴著一個「主語存在預設」,即主語S是存在的。及至19世紀末和20世紀初,一些學者開始用數學方法研究邏輯,形成「現代數理邏輯」。現代數理邏輯學家的研究對象雖然也包括量化句,但他們採用了全新的形式化表達方法,例如把「所有S是P」和「有S是P」分別表達為
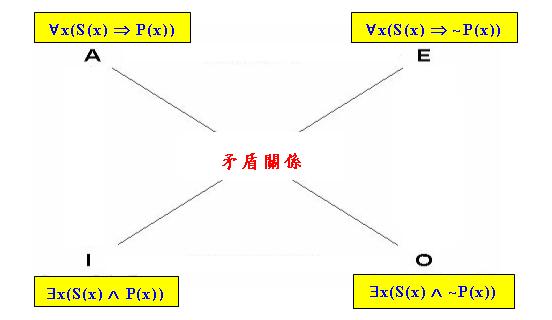
在這種新的表達法下,「主語存在預設」不再成立,導致傳統「對當關係推理」中的「差等關係」、「反對關係」與「下反對關係」也不再成立,上述「古典對當方陣」退化為以下的「布爾對當方陣」:
筆者曾經指出,我們可以把「主語S存在」設定為上述「古典對當方陣」中四句共有的「預設」,這是保留「對當關係推理」的一種方法。但除此以外,我們還有另一種改造「對當方陣」的方法,這就是把「古典對當方陣」中的「矛盾關係」、「(下)反對關係」和「差等關係」分別改為前面介紹的「外部否定關係」、「內部否定關係」和「對偶關係」。利用上述概念,當代的學者把「古典對當方陣」改造成以下的「新型對當方陣」(有些人又稱「對偶方陣」Square of Duality):

請注意上圖中的各種關係跟「古典對當方陣」中的關係具有不同的性質。舉例說,「全稱量詞」與「存在量詞」在「差等關係」下本來是不對稱的:
但在「對偶關係」下卻變成對稱的:
由於「對偶關係」是對稱的,所以上圖中A與I句以及E與O句之間的箭頭是雙向而非單向的,而且「對偶關係」的成立無需依賴「主語存在預設」(註1)。
我們還可以把上述「新型對當方陣」推廣為更一般的形式:

「對偶性推理」並不局限於一般量詞,而是存在於很多語言結構中。舉例說,筆者在上一章便曾介紹四個「體貌副詞」的各種否定關係,現在我們可以把這四個副詞排成以下「對當方陣」:

請注意上述副詞只適用於「新型對當方陣」而非「古典對當方陣」,這是因為「仍然」與「已經」之間並不存在「差等關係」。由此可見,「新型對當方陣」中的推理關係的確超出了傳統「對當關係推理」的內容。
為了更簡潔地表達「新型對當方陣」,Peters和Westerstahl在Quantifiers in Language and Logic一書中定義了一個函項Square (註2):設有「<1>型量詞」Q,則
例如
Peters和Westerstahl還證明了以下有關函項Square的定理。
| 定理1: | 以Square(Q)中任何一個元素作為Square的論元,所得結果等於原來的Square(Q),即若Q' ∈ Square(Q),則Square(Q') = Square(Q)。 |
容易證明上述定理是正確的,只需把~Q、Q~和Qd逐個代入(1)即可。舉例說,
| Square(~Q) | = {~Q, ~(~Q), (~Q)~, (~Q)d} |
| = {~Q, ~~Q, ~Q~, ~~Q~} |
| = {~Q, Q, Qd, Q~} |
| = Square(Q) |
其餘有關Square(Q~)和Square(Qd)的計算也類此,這裡從略。
根據「定理1」,我們知道
現在我們以Q<1>代表由所有「<1>型量詞」組成的集合,那麼「定理1」告訴我們,如果我們把Q<1>中的元素逐一代入(1),我們將得到Q<1>的一個「劃分」(Partition),即我們可以把Q<1>寫成
其中
根據集合論,每個Square(Qi)相當於Q<1>上的一個「等價類」(Equivalence Class),這些「等價類」是由以下二元關係「*」導出的:
容易看到上述定義的「*」確是一個「等價關係」(Equivalence Relation)。
從「定理1」的證明中,容易看到「外部否定」、「內部否定」以及「對偶」運算(還可加上一個「恆等」(Identity)運算,即把任何Q(#)(P)變成Q(#)(P)的運算)對於任意Square(Q)中的元素來說是封閉的。事實上,從「群論」(Group Theory)的角度看,上述四個運算構成一個「克萊因4元群」(Klein 4-Group)。如果我們把這四個運算看成這個群的元素,並把運算之間的「複合」(Composition) 看成這些元素之間的「乘法」(用。表示),那麼我們有以下「乘法表」(以下用ID、IN、ON和DU分別代表「恆等」、「內部否定」、「外部否定」和「對偶」):
| 。 | ID | IN | ON | DU |
|---|---|---|---|---|
| ID | ID | IN | ON | DU |
| IN | IN | ID | DU | ON |
| ON | ON | DU | ID | IN |
| DU | DU | ON | IN | ID |
由此可見,「新型對當方陣」具有深刻的集合論和群論意義。
筆者在上一章指出以下包含三層量詞的推理模式是有效的(在下式中,B代表「謂詞性論元」):
並指出上述推理模式實際上反映了「多重否定律」在下式中的運用:
請注意在上式中,置於中間的量詞Q'必須在上式右端轉化為~Q'~,才能剛好抵消處於其前及其後的兩個「~」。如果在上式中,我們把Q'保持原狀不變,所得結果不是有效的推理模式:
這是因為在上式中,兩個「~」不能隔著中間的Q'而互相抵消。換句話說,在一般情況下,
不是有效的推理模式。
不過上述情況卻有一個例外,假如Q'(#')是本身的「對偶」,那麼(2)便是有效的推理模式。為此,我們需要引入「自對偶」(Self-Dual)的概念:「<1>型量詞」Q(#)是「自對偶」的當且僅當
請注意根據Q(#)d的定義,我們可以把上式變換為
接下來的任務便是找出哪些「<1>型量詞」是「自對偶」的,即找出哪些量詞滿足(4)的等式。首先,我們知道「專有名詞」滿足(4),這可以從以下等價關係看出:
以下給出一個形式證明。根據《廣義量詞系列:基本單式量詞》,我們可以把「專有名詞」"John"表達為"every({j})",而"every({j})"的「外部否定」和「內部否定」分別為"(not every)({j})"和"no({j})"。根據這兩個「<1>型量詞」的真值條件以及「單元集」的性質,我們有
| (not every)({j})(B) | |
| ⇔ | {j} ∩ ~B ≠ Φ |
| ⇔ | {j} ⊆ ~B |
| ⇔ | {j} ∩ B = Φ |
| ⇔ | no({j})(B) |
由此證明了"every({j})"滿足(4)。請注意對於形如"every(A)" (其中A為任意集合)的量詞,上述推理並不成立,因此一般的「全稱量化名詞組」不是「自對偶」的。
確立了「專有名詞」的「自對偶」性質,我們便可以構造一些涉及「專有名詞」的「對偶性推理」,例如我們可以把「專有名詞」套用於上面(2)中的Q'(#'),從而得到以下推理實例:
其次,「反身代名詞」也是「自對偶」的。筆者在《廣義量詞系列:非迭代多式量詞》中介紹了「普通反身化算子」和「領屬反身化算子」,以下只集中討論形式為[self1(−)]2的「普通反身化算子」,這種「反身化算子」代表那些在含有三元謂詞的句式中處於第二論元位置並且與第一論元同指的「反身代名詞」,例如"Every boy bought himself at most 3 gifts."中的"himself"。根據上述網頁,設B(x, y, z)為三元謂詞,那麼
如果我們把[self1(−)]2看作「<1>型量詞」,那麼我們可以仿照普通「<1>型量詞」定義其「外部否定」和「內部否定」如下:
接著讓我們證明上述兩個集合是等價的。根據上述定義,對於任何(x, z)而言,我們有
| (x, z) ∈ [~self1(−)]2(B) | |
| ⇔ | (x, z) ∈ ~{(x, z): B(x, x, z)} |
| ⇔ | (x, z) ~∈ {(x, z): B(x, x, z)} |
| ⇔ | ~B(x, x, z) |
| ⇔ | (x, z) ∈ {(x, z): ~B(x, x, z)} |
| ⇔ | (x, z) ∈ [self1(−)]2(~B) |
| ⇔ | (x, z) ∈ [self1(−)~]2(B) |
由於(x, z)和B是任意的,我們證明了[~self1(−)]2 ≡ [self1(−)~]2,從而證明了[self1(−)]2是「自對偶」的。請注意我們可以把上述證明推廣至其他形式的「普通反身化算子」以及各種形式的「領屬反身化算子」。至此我們證明了普通格和所有格的「反身代名詞」是「自對偶」的。把「反身代名詞」套用於(2)中的Q'(#'),我們可以得到以下推理實例:
最後,當n為奇數時,我們還可以構造一組形式為"(Q of the n)(A)"的「「自對偶部分格結構」,在這裡「Q」代表一個數詞或多個數詞的析取,A則是「名詞性論元」。設|A| = n = 2k + 1,並設f為把{0, ... k}映射到{0, 1}的函數,那麼我們可以定義以下「<1>型量詞」F(A):
| [F(A)](B) = | f(|A ∩ B|), | if 0 ≤ |A ∩ B| ≤ k | (5) |
| 1 − f(n − |A ∩ B|), | if k + 1 ≤ |A ∩ B| ≤ 2k + 1 |
由於把{0, ... k}映射到{0, 1}的函數共有2k+1個,當|A| = 2k + 1時,我們可以根據上式構造2k+1個「<1>型量詞」。
接著讓我們看看上述量詞的一些實例。設n = 7 (即k = 3),並設f: 0 → 0, 1 → 0, 2 → 0, 3 → 0,那麼根據(5),我們有以下「<1>型量詞」F1(A):
| [F1(A)](B) = | 0, | if 0 ≤ |A ∩ B| ≤ 3 |
| 1, | if 4 ≤ |A ∩ B| ≤ 7 |
請注意以上這個量詞可以表述為"(more than 3 of the 7)(A)",容易驗證這個量詞是「自對偶」的,因為若在A的7個元素中,多於3個(即4至7個)不具有性質B,那麼必有0至3個元素具有性質B,亦即具有性質B的元素的數目不多於3。換句話說,(more than 3 of the 7)(A)~ ≡ ~(more than 3 of the 7)(A)。
讓我們再看另一個例子。設n = 7,並設f: 0 → 0, 1 → 1, 2 → 1, 3 → 0,那麼根據(5),我們有以下「<1>型量詞」F2(A):
| [F2(A)](B) = | 1, | if |A ∩ B| ∈ {1, 2, 4, 7} |
| 0, | if |A ∩ B| ∈ {0, 3, 5, 6} |
請注意以上這個量詞可以表述為"(exactly 1 or 2 or 4 or all of the 7)(A)",容易驗證這個量詞也是「自對偶」的,因為若在A的7個元素中,有1或2或4或7個不具有性質B,那麼必有6或5或3或0個元素具有性質B,亦即具有性質B的元素的數目不是1或2或4或7。換句話說,(exactly 1 or 2 or 4 or all of the 7)(A)~ ≡ ~(exactly 1 or 2 or 4 or all of the 7)(A)。
在上述例子中,量詞"(exactly 1 or 2 or 4 or all of the 7)(A)"給我們提供了兩個集合:{1, 2, 4, 7}和{7 − 1, 7 − 2, 7 − 4, 7 − 7} = {6, 5, 3, 0},這兩個集合互斥,而且這兩個集合的并集剛好等於{0, ... 7}。請注意上述例子的情況正是形式為"(Q of the n)(A)"的「自對偶部分格結構」必須滿足的條件,即這類量詞必須能表述為"(exactly n1 or ... nm of the n)(A)"的形式,其中{n1, ... nm}與{n − n1, ... n − nm}互斥,而且這兩個集合的并集剛好等於{0, ... n}。根據上述條件,我們知道只有在n為奇數的情況下,"(Q of the n)(A)"才可能是「自對偶」的。
接著讓我們證明在n為奇數的情況下,(5)所定義的量詞確是「自對偶」的。首先,由於[F(A)~](B) = [F(A)](~B)以及A ∩ ~B = A − B,根據(5),我們有
| [F(A)~](B) = | f(|A − B|), | if 0 ≤ |A − B| ≤ k |
| 1 − f(n − |A − B|), | if k + 1 ≤ |A − B| ≤ 2k + 1 |
另一方面,由於n = 2k + 1 = |A| = |A ∩ B| + |A − B|,我們必有
因此我們可以把上式改寫為
| [F(A)~](B) = | f(n − |A ∩ B|), | if k + 1 ≤ |A ∩ B| ≤ 2k + 1 |
| 1 − f(|A ∩ B|), | if 0 ≤ |A ∩ B| ≤ k |
可是,上式正好是[~F(A)](B) = 1 − [F(A)](B)的定義,由此得~F(A) ≡ F(A)~,即這個量詞是「自對偶」的。把前述的"(more than 3 of the 7)(A)"套用於(2)中的Q'(#'),我們可以得到以下推理實例:
在本節我們探討另一種具有特殊性質的量詞。回顧上面的(3),如果我們把該等式中的Q(#)d改為Q(#)~,我們將有一種新的關係:
我們把符合上述關係的「<1>型量詞」稱為「內部否定不動點」(Fixed Point with respect to Inner Negation)(註3)。根據上述定義,「內部否定不動點」Q(#)滿足以下推理模式:
但除此以外,「內部否定不動點」還可應用於包含兩層或三層量詞的推理中,只要把筆者在上一章介紹的某些推理模式作適當修改便行了。舉例說,從以下推理模式
我們可以推導出「內部否定不動點」Q(#)滿足以下推理模式:
接下來的任務是找出各種「內部否定不動點」,即哪些「<1>型量詞」滿足(8)。Keenan在Further Excursions in Natural Logic: The Mid-Point Theorems一文中提出了以下的「中點定理」(Mid-Point Theorem)。
| 定理2: | 設p、q為分數,其中0 ≤ p ≤ q ≤ 1並且p + q = 1,則「<1>型量詞」"(between p and q)(A)"和"(more than p but less than q)(A)"是「內部否定不動點」。特別地,當p = q = 1/2時,p和q滿足上述條件,因此"(exactly half)(A)"也是「內部否定不動點」。 |
請注意若p、q符合上述定理的條件,則1/2 − p = q − 1/2,即p和q離開[0, 1]的「中點」1/2的距離相等,故此一定理稱「中點定理」。
以下用「反證法」來證明上述定理,為方便行文,以下設定|A ∩ B| / |A| = k,那麼根據集合論,|A − B| / |A| = 1 − k。設p、q符合上述條件,並且(between p and q)(A)(B),即k ∈ [p, q]。現假設(between p and q)(A)(~B)不成立,即1 − k不在[p, q]之內,亦即1 − k < p或1 − k > q。由於p + q = 1,從上述結果我們可推得k > q或k < p,與k ∈ [p, q]矛盾。由此證得(between p and q)(A)(B) ⇒ (between p and q)(A)(~B),同理亦易證(between p and q)(A)(~B) ⇒ (between p and q)(A)(B)。綜合以上結果,我們證明了"(between p and q)(A)"是「內部否定不動點」。只要把上述證明中的「閉區間」[p, q]換成「開區間」(p, q),便可證明"(more than p but less than q)(A)"也是「內部否定不動點」。
請注意由於「部分格結構」也可看成某種「相對數量詞」,「中點定理」也適用於這類量詞,即設|A| = n,l、m為自然數,0 ≤ l ≤ m ≤ n並且l + m = n,則"(between l and m of the n)(A)"和"(more than l but fewer than m of the n)(A)"是「內部否定不動點」。利用「定理2」以及(9)-(10),我們可以得到以下推理實例:
筆者在《廣義量詞系列:基本單式量詞》中介紹了「布爾量詞」的概念,即用「(外部)否定」、「合取」和「析取」這三種「布爾運算」從較簡單量詞複合而成的量詞。根據Keenan和Faltz合著的Boolean Semantics for Natural Language一書,「布爾運算」可以作用於多種語言結構,而作用於不同結構上的「布爾運算」可能有不同的意義。對於「<1>型量詞」Q(#)和Q'(#')而言,上述三種「布爾運算」的意義為:
我們有以下定理。
| 定理3: | 「內部否定不動點」在「布爾運算」下是封閉的,即若Q(#)和Q'(#')是「內部否定不動點」,則~Q(#)、(Q(#) ∧ Q'(#'))和(Q(#) ∨ Q'(#'))也是「內部否定不動點」。 |
以下讓我們證明上述定理。首先,設Q(#)為「內部否定不動點」,則有
| (~Q(#))~(B) | |
| ⇔ | (~Q(#))(~B) |
| ⇔ | ~(Q(#)(~B)) |
| ⇔ | ~(Q(#)~(B)) |
| ⇔ | ~(Q(#)(B)) |
| ⇔ | (~Q(#))(B) |
即~Q(#)也是「內部否定不動點」。其次,設Q(#)和Q'(#')為「內部否定不動點」,則有
| (Q(#) ∧ Q'(#'))~(B) | |
| ⇔ | (Q(#) ∧ Q'(#'))(~B) |
| ⇔ | Q(#)(~B) ∧ Q'(#')(~B) |
| ⇔ | Q(#)~(B) ∧ Q'(#')~(B) |
| ⇔ | Q(#)(B) ∧ Q'(#')(B) |
| ⇔ | (Q(#) ∧ Q'(#'))(B) |
即(Q(#) ∧ Q'(#'))也是「內部否定不動點」。同理亦易證(Q(#) ∨ Q'(#'))也是「內部否定不動點」,「定理3」得證。
利用「定理3」,我們可以從已有的「內部否定不動點」推導出其他「內部否定不動點」。舉例說,根據「定理2」,設0 ≤ p ≤ q ≤ 1並且p + q = 1,則"(between p and q)(A)"是「內部否定不動點」。由於「內部否定不動點」在「(外部)否定」運算下封閉,由此可知上述量詞的「外部否定」"(more than q or less than p)(A)"也是「內部否定不動點」。同樣,我們亦知道"(exactly half)(A) ∧ (between 4 and 6 of the 10)(B)"是「內部否定不動點」,因為此一量詞是兩個「內部否定不動點」的「合取」。由此我們有以下推理實例:
Keenan在上述文章中還提出了以下的「廣義中點定理」(Generalized Mid-Point Theorem)。
| 定理4: | 設Q(#)為「<1>型量詞」,則「布爾量詞」(Q(#) ∧ Q(#)~)和(Q(#) ∨ Q(#)~)是「內部否定不動點」。 |
上述定理不難證明,設B為任意「謂詞性論元」,則有
| (Q(#) ∧ Q(#)~)~(B) | |
| ⇔ | (Q(#) ∧ Q(#)~)(~B) |
| ⇔ | Q(#)(~B) ∧ Q(#)~(~B) |
| ⇔ | Q(#)(~B) ∧ Q(#)(B) |
| ⇔ | Q(#)~(B) ∧ Q(#)(B) |
| ⇔ | (Q(#) ∧ Q(#)~)(B) |
即(Q(#) ∧ Q(#)~)是「內部否定不動點」,同理也易證(Q(#) ∨ Q(#)~)是「內部否定不動點」。
請注意在上述定理中,各個「布爾量詞」的兩個「名詞性論元」必須是同一個「#」,否則該定理不成立。但由於「布爾運算」具有以下性質:
我們可以把這些量詞中的「布爾運算」從「<1>型量詞」的層面提升至「<1,1>型量詞」的層面。舉例說,我們可以把"all boys or no boys"改寫為"all or no boys",即把這裡的"or"從連接兩個名詞短語的連詞提升為連接兩個限定詞的連詞,以下筆者將採用這種方式處理這種「布爾量詞」。
利用「定理4」,我們可以發掘出更多「內部否定不動點」。舉例說,由於"(exactly q)(A)"與"(exactly (1 − q))(A)" (其中q為分數)互為「內部否定」形式,我們知道"(exactly q or (1 − q))(A)"是「內部否定不動點」。此一結果還可推廣至「部分格結構」,從而推知"(exactly m or (n − m) of the n)(A)"也是「內部否定不動點」。我們有以下推理實例:
請注意在上述量詞中,q和(1 − q)離開1/2的距離以及m和(n − m)離開n/2的距離各自相等,所以「定理4」稱為「廣義中點定理」。
我們還可以對上一章介紹的其他量詞綜合運用「定理3」和「定理4」,從而構造出各種「內部否定不動點」。舉例說,我們可以根據「定理4」把互為「內部否定」的"all(A)"與"no(A)"組合成「內部否定不動點」"(all or no)(A)",然後再應用「定理3」推知上述量詞的「外部否定」"(some but not all)(A)"也是「內部否定不動點」。
請注意「定理4」只告訴我們理論上可以把哪些量詞配對,但實際上某些組合可能會產生「平凡量詞」。舉例說,儘管"all(A)"與"no(A)"以及"some(A)"與"(not all)(A)"互為「內部否定」形式,但在自然語言中卻不存在"(all and no)(A)"或"(some or not all)(A)"這樣的量詞,這是因為這兩個量詞是「平凡量詞」:前者與任何「謂詞性論元」B結合後皆為假命題,相當於「永假量詞」"0(A)";而後者與任何B結合後均為真命題,相當於「永真量詞」"1(A)" (註4)。
事實上,上述情況可以用「對當方陣」加以解釋。在「對當方陣」上,「內部否定」相當於兩種關係:「反對關係」和「下反對關係」,這兩種關係分別為「不可同真」和「不可同假」的關係,因此若「<1,1>型量詞」Q和Q'存在「反對關係」,則(Q ∧ Q')(A)相當於"0(A)";若Q和Q'存在「下反對關係」,則(Q ∨ Q')(A)相當於"1(A)" (註5)。回顧「古典對當方陣」,我們看到"all"與"no"存在「反對關係」,而"some"與"(not all)"則存在「下反對關係」,這就解釋了為何"(all and no)(A)"和
"(some or not all)(A)"相當於「平凡量詞」了。由此可見,在構造「內部否定不動點」時,除了應用「定理4」外,我們還須應用「對當方陣」的知識,以避免構造出「平凡量詞」,這顯示現代的「對偶性推理」與古典「對當關係推理」存在微妙的關係。
在本章和上一章,筆者介紹了「外部否定」和「內部否定」的概念(以及兩者的複合-「對偶」),這兩種否定分別相當於筆者在《廣義量詞系列:單調性推理原理》中介紹的「算子否定」和「論元否定」。對於「<1,1>型量詞」而言,「論元否定」可以作用於兩種對象。到目前為止筆者討論的「內部否定」其實只相當於「右論元否定」。一個自然的推論是,是否可以把「左論元否定」引入「對偶性推理」中?答案是肯定的。
為了區別兩種「論元否定」,由現在開始筆者將把此前討論的「內部否定」改稱為「右論元否定」(Right-Argument Negation,又可稱為「謂語否定」);而把本節討論的否定稱為「左論元否定」(Left-Argument Negation,又可稱為「主語否定」)。設有「<1,1>型量詞」Q,「左論元否定」就是把語句「Q(A)(B)」變成「Q(~A)(B)」的變換(註6)。為簡化寫法,筆者將把Q的「左論元否定」記作Q~l (而Q的「右論元否定」則記作Q~r,這裡下標中的"l"和"r"分別為"left"和"right"的縮寫),即
一般而言,我們可以在某一「<1,1>型量詞」的「名詞性論元」前加"non-" (相當於漢語的「非」)以得到該量詞的「平凡左論元否定」形式。除此以外,在自然語言中某些「<1,1>型量詞」還具有「非平凡左論元否定」形式。從直觀上看,只要我們把某一語句的兩個論元顛倒並把有關量詞換成其「逆向反義詞」,便可從「右論元否定」得到「左論元否定」,例如我們可以把語句「every(A)(~B)」變換為「only(~B)(A)」。由於根據上一章的表2,"every"與"no"互為「右論元否定」形式,即
而"no"具有「對稱性」,即
由此可得到
即"only"與"no"互為「左論元否定」形式。上述討論顯示,「非平凡左論元否定」形式可以從某些「<1,1>型量詞」的「逆向反義詞」中尋。下表列出某些常用「<1,1>型量詞」的「逆向反義詞」及其真值條件(在下表中,l、m、n為自然數,且0 < l < m < n,p、q為分數,且0 < p < q < 1,X代表「語境集」)(註7):
| 論元結構 | 真值條件 |
|---|---|
請注意從語法上說,上表所列的量詞跟一般「<1,1>型量詞」不同,它們都不是「限定詞」,例如在傳統語法中,"only"一般被分析為副詞,而"(constitute at least m of the n)"等則是「動詞 + 限定詞」結構(筆者在這裡把「(constitute at least m of the n)(A)(B)」規定為語句"A constitutes at least m of the n B."的論元結構)。不過,由於這些結構可作為某些常用「<1,1>型量詞」的「逆向反義詞」出現於「對偶性推理」中,所以本文把這些結構處理成某種抽象的「<1,1>型量詞」。
根據上表,我們可以得到某些「<1,1>型量詞」的「非平凡外部否定」和「非平凡左論元否定」形式,如下表所示:
| 量詞 | 「外部否定」形式 |
|---|---|
| 量詞 | 「左論元否定」形式 |
|---|---|
類似「右論元否定」,我們可以推導出涉及「左論元否定」的推理模式。根據「左論元否定」的定義,我們有以下推理模式:
利用上述模式和表3,我們有以下推理實例:
我們能否把上述推理模式推廣為包含兩層量詞的「左論元否定」推理模式?回顧上一章,包含兩層量詞的「右論元否定」推理模式都是涉及「迭代量詞」的推理,而「迭代量詞」的「迭代」運算都是作用於「右論元」上,例如以下語句
可以表達為以下「迭代」形式:
其中some(GIRL)(LOVE)處於外層「三分結構」的「右論元」位置。現在的問題是,哪一種語言結構可被表達為作用於「左論元」上的「迭代」運算?答案就是某些帶有「定語分句」的語句。試看以下例句:
請注意上句存在岐義,這視乎"only"是以甚麼作為其焦點。假如上句的焦點結構如下所示(以下用[ ]F括出焦點):
即整個名詞短語"boys who love some girl"都在"only"的焦點內,那麼語句(12)的意思是:除了那些愛至少一個女孩的男孩外,沒有其他個體(包括不愛任何女孩的男孩以及非男孩)出席。在這種解讀下,(12)應被表達為以下「迭代三分結構」:
可是(12)還可以有另一種焦點結構,如下所示:
即只有關係分句"who love some girl"在"only"的焦點內。在這種焦點結構下,語句(12)的意思是:在男孩之中,除了那些愛至少一個女孩的男孩外,沒有其他男孩出席,但並不排除有其他非男孩出席。以下筆者將主要討論在第二種解讀下語句(12)的「對偶性推理」。現以下圖說明語句(12)的第二種解讀的意思:

在上圖中,L代表集合{x: some(GIRL)({y: LOVE(x, y)})},我們可以把(12)的第二種解讀視為陳述紅色粗框包著的範圍(而非整幅圖)的情況,這相當於把(12)的論域從U縮小為BOY (即紅色粗框包著的範圍)。把論域限制在BOY後,我們便可以把(12)的第二種解讀表達為
在上式中,"(onlyU|BOY)"表示對量詞"only"的「限制」(Restriction)操作,「限制」操作的定義為:若Q為論域U上的「<1,1>型量詞」,S為任何集合,則
根據上述定義,"(onlyU|BOY)"的意思就是把"only"的論域從原來的U改為BOY,並把BOY與"only"的原來兩個論元相交(這是要確保兩個新的論元為BOY的子集)。由於論域已改為BOY,因此對(14)中的第一論元進行的否定運算也是相對於BOY而言的,即
| ~{x: some(GIRL)({y: LOVE(x, y)})} | |
| = | BOY ∩ ~{x: some(GIRL)({y: LOVE(x, y)})}} |
| = | BOY ∩ {x: no(GIRL)({y: LOVE(x, y)})}} |
| = | {x: no(GIRL)({y: LOVE(x, y)})}} |
把(14)應用於(11),我們便會得到以下與(14)等價的「三分結構式」:
由此得到以下推理實例:
仿照其他否定概念,我們也可以定義「左論元否定不動點」(Fixed Point with respect to Left-Argument Negation),這是指滿足以下條件的「<1,1>型量詞」Q:
根據上述定義,「左論元否定不動點」Q滿足以下推理模式:
接下來讓我們找出各種「左論元否定不動點」,即滿足(15)的「<1,1>型量詞」。由於「左論元否定」是「右論元否定」的逆向反義概念,我們只要把第4節的「定理2」至「定理4」作適當修改,便可得到有關「左論元否定不動點」的下列定理。
| 定理5: | 設p、q為分數,其中0 ≤ p ≤ q ≤ 1並且p + q = 1,則「<1,1>型量詞」"(constitute between p and q)"和"(constitute more than p but less than q)"是「左論元否定不動點」。特別地,當p = q = 1/2時,p和q滿足上述條件,因此"(constitute exactly half)"也是「左論元否定不動點」。
|
| 定理6: | 「左論元否定不動點」在「布爾運算」下是封閉的,即若Q和Q'是「左論元否定不動點」,則~Q、(Q ∧ Q')和(Q ∨ Q')也是「左論元否定不動點」。
|
| 定理7: | 設Q為「<1,1>型量詞」,則「布爾量詞」(Q ∧ Q~l)和(Q ∨ Q~l)是「左論元否定不動點」。 |
請注意「定理5」亦適用於「部分格結構」。利用上述定理,我們便可以構造出各種「左論元否定不動點」。舉例說,根據「定理5」,我們推知"(constitute between 1/3 and 2/3)"是「左論元否定不動點」。根據「定理7」和表3,我們推知"(only or no)"是「左論元否定不動點」;再根據「定理6」,可知上述量詞的「外部否定」"(some but not restricted to)"也是「左論元否定不動點」(註8)。把上述量詞應用於(16),便可得到以下推理實例:
我們還可以把"(only or no)"應用於包含兩層量詞的「左論元否定」推理中,例如
我們還可以繼續推廣上述否定概念,既然已有「右論元否定」和「左論元否定」的概念,那麼我們也可以定義「左右論元否定」(Left and Right-Argument Negation,又可稱為「主謂否定」)的概念。以下筆者把這種否定記作Q~lr,其定義如下:
根據上述定義,我們知道「左右論元否定」有以下推理模式:
自然語言中有哪些「<1,1>型量詞」具有「非平凡左右論元否定」形式?由於這種否定是「右論元否定」和「左論元否定」的複合,我們可以從具有這兩種否定的「非平凡形式」的量詞中尋。根據表3,"only"和"(apart from John only)"各有「非平凡左論元否定」形式,分別為"no"和"(no except John)";而根據上一章,這後兩個量詞又各有「非平凡右論元否定」形式,分別為"every"和"(all except John)",由此我們得到以下結果:
| 量詞 | 「左右論元否定」形式 |
|---|---|
把上表所示量詞應用於(17),便可得到以下推理實例:
我們還可以構造包含兩層量詞的「左右論元否定」推理。舉例說,語句
可被表達為
把上式應用於(17),便可得到以下推理實例:
我們也可以定義「左右論元否定不動點」(Fixed Point with respect to Left and Right-Argument Negation)的概念,即滿足以下條件的「<1,1>型量詞」Q:
根據上述定義,「左右論元否定不動點」Q滿足以下推理模式:
由於「左右論元否定」是「右論元否定」和「左論元否定」的複合,容易看到這種否定也有類似「定理6」和「定理7」的定理。
| 定理8: | 「左右論元否定不動點」在「布爾運算」下是封閉的,即若Q和Q'是「左右論元否定不動點」,則~Q、(Q ∧ Q')和(Q ∨ Q')也是「左右論元否定不動點」。
|
| 定理9: | 設Q為「<1,1>型量詞」,則「布爾量詞」(Q ∧ Q~lr)和(Q ∨ Q~lr)是「左右論元否定不動點」。 |
利用「定理9」和表4,我們推知"(all and only)"是「左右論元否定不動點」;再根據「定理8」,可知上述量詞的「外部否定」"(not all or not only)"也是「左右論元否定不動點」。以下僅舉涉及"(all and only)"的一個推理實例:
「對偶」和「左右論元否定」是兩種否定的複合,前者是「外部否定」與「右論元否定」的複合,後者則是「左論元否定」與「右論元否定」的複合。一個自然的推論是,應該還可定義其他複合否定概念。首先,我們可以把「外部否定」與「左論元否定」複合,從而得到一種新的「對偶」。為區別新舊兩種「對偶」,現把此前介紹的「對偶」改稱「右對偶」(Right Dual),並把本小節介紹的「對偶」稱為「左對偶」(Left Dual),記作Qld (而Q的「右對偶」則記作Qrd),其定義為
根據上述定義,「左對偶」有以下推理模式:
接著我們可以利用表2和表3求得某些量詞的「非平凡左對偶」形式:
| 量詞 | 左對偶 |
|---|---|
利用上表,我們可以得到以下推理實例:
類似第3節介紹的「自對偶」(以下改稱「右自對偶」Right Self-Dual),我們也可定義「左自對偶」(Left Self-Dual)的概念,即滿足以下條件的「<1,1>型量詞」Q:
根據上述定義,「左自對偶」量詞Q滿足以下推理模式:
請注意我們可以沿用3.2.3小節的公式(5)以得到形式為"(constitute Q of the n)"的「左自對偶」量詞,只要把該公式中A和B的角色對調便行了。根據3.2.3小節的討論,我們知道"(constitute more than 3 of the 7)"是「左自對偶」量詞,從而有以下推理實例:
其次,我們可以把三種否定(「外部否定」、「左論元否定」和「右論元否定」)複合,筆者把這種複合稱為「左右對偶」(Left and Right Dual),記作Qlrd,其定義為
根據上述定義,「左右對偶」有以下推理模式:
鑑於此一概念涉及三重否定,在自然語言中究竟是否有量詞具有「非平凡左右對偶」形式?根據表4,"every"與"only"互為「左右論元否定」形式,由此可以求得這兩個量詞的「左右對偶」為:
| 量詞 | 左右對偶 |
|---|---|
但問題是,此前筆者一直不把"(not all)"和"(not only)"視作「非平凡外部否定」形式,因此嚴格地說,自然語言中沒有量詞具有「非平凡左右對偶」形式。不過即使如此,也不阻礙我們進行「左右對偶」推理,例如:
接著我們研究哪些量詞是「左右自對偶」(Left and Right Self-Dual)量詞,即滿足以下條件的「<1,1>型量詞」Q:
首先,從表6可見,只有極少量詞具有「非平凡左右對偶」形式,而且這些量詞都不是「左右自對偶」量詞。其次,對於「左右對偶」運算來說,沒有類似「定理4」的定理,即對表6的量詞進行「布爾運算」,也不能得到「左右自對偶」量詞。由此可以推斷,自然語言中不存在「左右自對偶」量詞。
最後,筆者還要指出,「外部否定不動點」(Fixed Point with respect to Outer Negation)也是不存在的。「外部否定不動點」是指滿足以下條件的「<1>型量詞」Q(#):
以下讓我們用「反證法」來證明沒有量詞可滿足上述條件,故設存在這樣的量詞Q(#),那麼對於任何「謂詞性論元」B,都有
但上式是不可能成立的,因為任何命題「Q(#)(B)」都不可能與其否定命題等價。
至此筆者已把上一章介紹的三種否定運算擴充為七種,現把這七種否定運算(另加一個「恆等」運算)的定義總結成下表:
| 運算 | 定義 | ||
|---|---|---|---|
| 量詞 | 左論元 | 右論元 | |
理論上,給定一個「<1,1>型量詞」Q,我們可以找出與Q相應的七個否定形式。舉例說,給定"every",我們除了可找出上一章已介紹的三種相應否定形式(即「右論元否定」形式"no"、「外部否定」形式"(not every)"和「右對偶」形式"some"外,我們還可以找出其餘四種否定形式,即「左論元否定」形式"(every non-)"、「左右論元否定」形式"only"、「左對偶」形式"(not every non-)"和「左右對偶」形式"(not only)"。請注意上面列舉的量詞有一些不太自然或一般不被看作一個語言單位,例如"(every non-)"。不過為了使本節的討論完整,這裡姑且把這些詞項當作普通「<1,1>型量詞」處理。事實上,這些詞項像其他量詞一樣具有明確的真值條件,例如"(every non-)"的真值條件就是:
利用"every"以及上述七個否定形式,我們便可以把前述的「新型對當方陣」擴大為以下的「對當立方體」(Cube of Opposition)(註9):

上圖沒有列出立方體中每一對頂點之間的關係,這是因為該立方體的八個頂點共可構成C(8, 2) = 28個對子,如果把這28個對子的關係全部列於上圖,將使上圖非常雜亂。不過要推導這28個關係其實不難,首先我們像上面2.2小節那樣構造上述八種運算之間的「乘法表」(以下用ID、RN、ON、RD、LN、LRN、LD和LRD分別代表「恆等」、「右論元否定」、「外部否定」、「右對偶」、「左論元否定」、「左右論元否定」、「左對偶」、「左右對偶」):
| 。 | ID | RN | ON | RD | LN | LRN | LD | LRD |
|---|---|---|---|---|---|---|---|---|
| ID | ID | RN | ON | RD | LN | LRN | LD | LRD |
| RN | RN | ID | RD | ON | LRN | LN | LRD | LD |
| ON | ON | RD | ID | RN | LD | LRD | LN | LRN |
| RD | RD | ON | RN | ID | LRD | LD | LRN | LN |
| LN | LN | LRN | LD | LRD | ID | RN | ON | RD |
| LRN | LRN | LN | LRD | LD | RN | ID | RD | ON |
| LD | LD | LRD | LN | LRN | ON | RD | ID | RN |
| LRD | LRD | LD | LRN | LN | RD | ON | RN | ID |
利用上表,我們便可以推導上圖中任何一對頂點之間的關係。舉例說,由於"no"與"(not only)"分別為"every"的「右論元否定」(RN)和「左右對偶」(LRD)形式,根據上表,LD。RN = LRD並且LD。LRD = RN,這即是說,當我們把「no(A)(B)」變換為「~no(~A)(B)」後,便會得到「(not only)(A)(B)」,反之亦然。由此可知,"no"與"(not only)"之間存在「左對偶」關係。
理論上,我們還可以仿照2.2小節所介紹的,定義一個函項Cube:設有「<1,1>型量詞」Q,則
例如
當然,在自然語言中我們不容易找到齊備上列八個形式的「<1,1>型量詞」,因此上述函項一般只有理論意義,筆者不擬深入討論。
到目前為止,筆者所介紹的「對偶性推理」都是「直接推理」,即從一個前提直接推出結論的推理。Keenan在Excursions in Natural Logic一文中提出了一個定理,涉及由兩個前提推出結論的推理模式,後來Westerstahl改良了這個定理,現把這個定理引述如下。
定理10:設Q為「右守恆」的「<1,1>型量詞」,則Q是「右遞增」的當且僅當以下推理成立:
| 前提1: | Q(A)(B) | (24) (註10) |
| 前提2: | Q(A)d(C) | |
| 結論: | some(A)(B ∩ C) |
筆者把上述推理模式稱為「對偶三段論」,以下是上述推理模式的一個實例(請注意"(more than 2/3)"是「右守恆」和「右遞增」量詞):
| 前提1: | 超過三分二會員出席了會議。 |
| 前提2: | 至少三分一會員是女性。 |
| 結論: | 有會員是女性且出席了會議。 |
上述定理須用到「右守恆性」和「右遞增性」的概念,其中「右遞增性」以及下文將須用到的「左遞增性」在《廣義量詞系列:單調性推理原理》中已有所介紹。至於「右守恆性」以及下文將會介紹的「左守恆性」,這裡只提供簡單定義,筆者以後還會詳細討論這兩種性質。設Q為「<1,1>型量詞」,A、B為集合,則Q是「右守恆」(Right Conservative)的當且僅當
Q是「左守恆」(Left Conservative)的當且僅當
接著讓我們證明上述定理。首先設Q為「右遞增量詞」,並且Q(A)(B)和Q(A)d(C)真,我們用「反證法」來證明some(A)(B ∩ C)也真,故設此一結論不真,即A ∩ B ∩ C = Φ,則有A ∩ B ⊆ ~C。從Q的「右守恆性」以及Q(A)(B),可推得Q(A)(A ∩ B)真。再根據Q的「右遞增性」,必有Q(A)(~C)真,即~(Q(A)(~C))假。但~(Q(A)(~C)) ≡ Q(A)d(C),即Q(A)d(C)假,這與前面的假設矛盾,由此我們證明了Q為「右遞增量詞」 ⇒ (24)有效。
其次設(24)為有效推理模式,並且B ⊆ B'和Q(A)(B)真,我們用「反證法」來證明Q(A)(B')也真,故設此一結論不真,則有Q(A)~(~B')假,即~(Q(A)~(~B'))真,但~(Q(A)~(~B')) ≡ Q(A)d(~B')。從(24)以及Q(A)(B)和Q(A)d(~B'),我們可以推出some(A)(B ∩ ~B'),即A ∩ B ∩ ~B' ≠ Φ。由此得B ∩ ~B' ≠ Φ,但這與B ⊆ B'矛盾。由此我們證明了(24)有效 ⇒ Q為「右遞增量詞」。綜合以上結果,「定理10」得證。
根據對稱性,我們還可以得到以下這個涉及「左對偶」的定理。
定理11:設Q為「左守恆」的「<1,1>型量詞」,則Q是「左遞增」的當且僅當以下推理成立:
| 前提1: | Q(A)(B) | (25) |
| 前提2: | Qld(C)(B) | |
| 結論: | some(A ∩ C)(B) |
上述定理的證明跟「定理10」大同小異,只須把該定理中的「右」改為「左」便行。以下是上述推理模式的一個實例例(請注意"only"是「左守恆」和「左遞增」量詞):
| 前提1: | 只有會員出席了會議。 |
| 前提2: | 有女性出席了會議。 |
| 結論: | 有女會員出席了會議。 |


