筆者在前面各章已先後介紹了「個體論域」、「時間論域」、「可能世界論域」、「命題論域」和「空間論域」下的各種量化結構,上述論域都是當今邏輯學和形式語義學的熱門研究領域。不過,筆者發現量化現象是自然語言中普遍存在的現象。通過類比推理,筆者發現除了上述論域外,量化現象還存在於其他較少人注意的語言結構中,包括「相關詞」和「度量」結構,本文的目的就是介紹這些量化結構。
筆者以往曾指出,最基本的「廣義量詞」(即<−,1>型和<1,1>型量詞)相當於自然語言的名詞短語和限定詞,因此如要發掘新的「廣義量化結構」,可以從自然語言的「代名詞-限定詞」系統(註1)入手。英語的「代名詞-限定詞系統」是一個種類龐雜的系統。根據傳統語法,英語的代名詞一般可分為「人稱代名詞」、「反身代名詞」、「指示代名詞」、「不定代名詞」(Indefinite Pronoun)(註2)、「疑問代名詞」(Interrogative Pronoun)、「關係代名詞」(Relative Pronoun)等多個次類。其中「疑問代名詞」和「關係代名詞」是兩個很特殊的類別,因為除了「疑問代名詞」和「關係代名詞」外,英語還有「疑問副詞」和「關係副詞」,包括表時間的"when"、表空間的"where"、表原因的"why"、表方式的"how"等(但"how"只能作「疑問副詞」,不能作「關係副詞」)。由此我們看到,「代名詞-限定詞系統」在某方面與某些副詞存在聯繫。
其實,如果我們把眼光放遠一點,我們便會看到在英語中,除了「疑問代名詞」和「關係代名詞」外,「指示代名詞」和部分「不定代名詞」也有對應的副詞。舉例說,對應於「指示代名詞」"that",有各種「指示副詞」,如表時間的"then"、表空間的"there"、表原因的"therefore"等。對應於「不定代名詞」"everyone"、"anyone"和"someone",也有各種「不定副詞」,包括表時間的"everytime"、"anytime"和"sometime";表空間的"everywhere"、"anywhere"和"somewhere"等。不過,英語的這種對應並不整齊,例如雖然有表時間和表空間的「不定副詞」,卻沒有表原因或表方式的「不定副詞」,即雖然有"everytime"、"everywhere",卻沒有"*everywhy"或"*everyhow" (但有"anyhow"和"somehow",雖然其意義並不純粹等於"any" + "how"和some" + "how")。當然英語可以用"for every reason"和"in every way"來表達"*everywhy"和"*everyhow"的意思,但"for every reason"和"in every way"是介詞短語,不能算作「不定副詞」。
漢語的「代詞」系統更能說明問題。在當今通行的漢語語法系統下,「代詞」主要是根據指代功能而非語法功能定義的。換句話說,所有具備指代功能的詞,不論其語法功能是作主語、賓語,還是作定語、狀語,都被歸入「代詞」。因此漢語的「代詞」便有一部分相當於英語語法中的「代名詞-限定詞」,例如「這」、「誰」、「哪個」等,另一部分則相當於英語語法中的「副詞」,例如「這兒」、「那樣」、「為甚麼」等。跟英語相似,漢語的「代詞」系統也是不整齊的。以表達「近指」的「代詞」為例,漢語有表個體的「這」、表時間的「這時」、表空間的「這兒」、表方式的「這樣」,但卻沒有表原因的「近指代詞」。如要表達此一意義,漢語要用短語「因為這個原因」表示(註3)。對於某些意義,漢語只有一個表個體的「代詞」。舉例說,在漢語中表達「不定指」意義的「代詞」便只有「某」,這個「代詞」是用來表達「不定指個體」。如要表達其他論域的「不定指」,便只能採取短語的形式,例如「某個地方」、「某個時間」、「某個原因」、「某個方式」等。
相比於英語的「代名詞-限定詞」系統和漢語的「代詞」系統,世界語(Esperanto)的「相關詞」(Correlative)系統(註4)便顯得非常整齊。現先把世界語的「相關詞」列於下表(請注意世界語的「疑問詞」和「關係詞」同形,其情況跟英語一樣):
| 人物/個體 | 事物 | 性質 | 領屬 | 時間 | 空間 | 原因 | 方式 | 數量 | |
|---|---|---|---|---|---|---|---|---|---|
| 集合(Collective) | |||||||||
| 不定(Indefinite) | |||||||||
| 否定(Negative) | |||||||||
| 指示(Demostrative) | |||||||||
| 疑問(Interrogative) | |||||||||
| 關係(Relative) |
上表顯示世界語的「相關詞」是一個結構完備的系統,表中沒有空白,各個「相關詞」的構形完全合符規律。現以以下例句說明世界語「相關詞」的特點:
| (1) | ||||||
| =「約翰用盡各種方法以得到『英雄』的稱號。」 |
由於世界語有一個相關詞"chiel"代表「集合 + 方式」,所以只需用一個單詞便可表達「以各種方式」的意思,而漢語因缺乏類似"chiel"的代詞,所以只好用短語「用盡各種方法」來表達此一意思。
表1的行和列分別對應著量化結構的不同方面。該表的每一行(「集合」、「不定」等)對應著某一種量詞或量化操作,其中「集合相關詞」、「不定相關詞」和「否定相關詞」分別對應著「全稱量詞」"every"、「存在量詞」"some"和「否定量詞」"no",這三個量詞正是「廣義量詞理論」中三個最基本的量詞。「指示相關詞」和「疑問相關詞」分別對應著筆者在《廣義量詞系列:特殊單式量詞》中介紹的「指示詞」和「疑問量詞」,這兩類詞的語義分別要應用到「語境函項」和「解答集」的概念。「關係相關詞」則用來構造筆者在《廣義量詞系列:迭代量詞》中介紹的「定語分句」(註6) 。以上這些內容在以前面各章中已詳細討論過了。
表1的每一列則代表著特定的論域,其中「人物/個體」、「事物」和「領屬」這三列合起來便相當於「個體論域」,「時間」和「空間」這兩列則分別代表前面數章介紹的「時間論域」和「空間論域」,餘下的四列則是筆者以往沒有討論過的領域,這些領域正是我們發掘新的論域的來源。以下就讓我們逐一考慮這些論域。
表1有一列以-om結尾的「數量相關詞」,用來表達多種數量意義。筆者認為對應於此一範疇,我們應有一個「數量論域」(Quantitative Domain,以下用QUAN表示)。可是這裡有一個問題,在「廣義量詞理論」中,「數量」概念一直是作為「量詞」的一部分而非獨立概念,「數量」一直是用來對其他論域的元素進行量化,它本身並非量化的對象。舉例說,數字n在「廣義量詞理論」中一般只作為量詞"(more than n)" 、"(exactly n)"、"(at most n)"等的一部分出現,本身沒有獨立地位。既然如此,那麼為何我們要把「數量」處理成獨立的論域?
事實上,在某些情況下,我們會把「數量」處理成語言表達式的主體而非量詞的一部分。其實筆者在《廣義量詞系列:特殊單式量詞》中介紹「疑問量詞」"(how many)"、"(what proportion of)"等時,便已隱含著「數量論域」,因為"(how many)"這類「疑問量詞」跟"who"、"what"等不同,後者是以人/物作為詢問對象,而前者則是以數量作為詢問對象。既然人/物可以構成「個體論域」,那麼數量自然也能構成「數量論域」。除了詢問數量的疑問句外,在某些數量比較句中,「數量」也構成表達式的主體。試看以下語句:
上句表達兩個數目之間的比較。如果我們用m和f分別代表「男生的數目」和「女生的數目」,那麼上句便可表達為下列「三分結構」:
請注意在上式中,m和f是數字,因此都是「數量論域」的元素。由此可見,「數量論域」確有其獨立存在的必要。
既然有「數量論域」,那麼我們也應有「數量論域」上的量詞(簡稱「數量量詞」),但這究竟是甚麼樣的量詞?首先,請注意表1中世界語的「數量相關詞」"chiom"、"iom"、"neniom"等分別表示「所有」、「有些」和「沒有」等意思,它們在本質上等同於「廣義量詞理論」中的"every"、"some"、"no",是用來對其他論域上的元素進行量化的量詞。試看以下例句:
| (註7) | |||||
| =「他犯了一些錯誤。」 |
在上句中,"iom da"相當於英語的"some",其量化對象是「個體論域」上屬於「錯誤」這個集合的元素。由此可見,世界語的大多數「數量相關詞」均非「數量量詞」(註8),那麼甚麼才是「數量量詞」?筆者認為,當我們在某些語言使用場合中對作為語言表達式主體的「數量」進行量化時,我們便是在使用「數量量詞」。試看以下例句:
撇除"any"的「任指」語義並把它當作等同於"every",那麼上句中的"any"便是「數量論域」上的「全稱量詞」,這是因為我們可以把上句理解為,對於「數量論域」QUAN上的每一個元素n而言(註9),n都是John可以借的圖書的數目。根據以上分析,我們可以把上句表達為以下「泛化量化結構」:
表1有一列以-a結尾的「性質相關詞」,用來表達"all kinds of"、"a certain kind of"、"what kind of"等意思。這些「相關詞」相當於對形容詞的量化,請注意這裡不是指對某一特定形容詞的量化,而是對某一語境下所有相關的形容詞的量化。舉例說,語句
的意思就是John接觸的人包括高的、矮的、肥的、瘦的、有禮貌的、無禮的、富有的、貧窮的......人,以上列舉的人的種類就是由各種形容詞表達的。若要用集合來表達上句中的"kinds",這個集合是由各種人的性質(如TALL、SHORT、FAT、THIN等等)組成的,因此筆者認為應引入「性質論域」(Property Domain,以下用符號PRO表示)的概念。在句法上,「性質」通常表現為「形容詞」。根據筆者在《廣義量詞系列:特殊單式量詞》中的分析,「形容詞」的類型是把集合映射到集合的「高階函項」,因此我們可以把PRO看成函項集合Power(U) → Power(U)的一個子集,其中Power(U)代表U的「冪集」。利用上述概念,我們便可以用形式化語言把上句中的"kinds"表達為
在上式中,P是代表「性質」的變項,上述集合的元素包括可用來描述人的「形容詞」,因此相當於人所具有的性質的集合。這樣,語句(2)便可以表達為以下「三分結構」:
由於上式中的第二論元是第一論元的真子集,上式中的量詞"every"可以改為「=」號,從而得到下式:
上式的意思是說,人所具有的性質的集合等同於John遇到的人所具有的性質的集合,這正是語句(2)的意思。
自然語言的形容詞除了可作為名詞修飾語外,亦可用來作謂語中心,而且自然語言中也存在詢問謂語中心的疑問句,例如
為了能表達這些疑問句(以及下文將要介紹的「焦點結構」),筆者認為應引入「謂詞論域」(Predicate Domain,以下用符號PRED表示)的概念。不過,自然語言中的謂詞可以有多種論元結構(例如以上兩句所詢問的謂詞便分別為一元謂詞和二元謂詞),因此從類型上說,這個論域的元素應是以下「并集」的一個子集:Power(U) ∪ Power(U2) ∪ ...,其中Power(U2)代表由U中所有二元謂詞組成的集合,其餘類推。利用上述概念,我們便可以用形式化語言把以上兩句表達為
表1有一列以-el結尾的「方式相關詞」,用來表達"in every way"、"in some way"、"in what way"等意思。請注意在這裡「方式」一詞亦包含「方法」(Means)/「工具」(Instrument)的意義。儘管「方式」與「方法」是兩個不同的概念,但在語言使用上,這兩個概念的分野有時並不清晰。在某些情況下,同一個詞在同一句中既可表達「方式」,又可表達「方法」。例如在以下語句中,
副詞"microscopically"便既可表達「方式」(意指「極細致地」),又可表達「方法」(意指「用顯微鏡」),甚或兩種意思兼備。由此可見,「方式」與「方法」在語義上有極密切的聯繫,因此本文把這兩個範疇統一為一個「方式論域」(Manner Domain,以下用MANN表示),並把「方式/方法」統稱為「方式」。
在英語中,「方式」常常表現為副詞」。在句法上,「方式副詞」都是作為動詞短語的修飾語,亦即「狀語」(註10)。因此從類型上說,「方式論域」的元素跟上述「性質論域」的元素相似,也是把集合映射到集合的「高階函項」。不過「方式論域」與「性質論域」仍有重要的區別。在邏輯上,形容詞所修飾的「普通名詞短語」一般都表現為一元謂詞;但「方式副詞」所修飾的「動詞短語」卻可表現為一元謂詞、二元謂詞等,例見以下語句:
因此,從類型上說,「方式副詞」應被分析為Power(U) ∪ Power(U2) ∪ ... → Power(U) ∪ Power(U2) ∪ ...的一個子集。基於上述分析,我們可以把上述三句表達為以下「三分結構」(在下式中,l代表"the letter"):
除了「方式副詞」外,「方式」亦常常表現為「方式介詞短語」,例如"with the stick",這些介詞短語也應被分析成「方式論域」的元素,即「高階函項」。至於「方式介詞」(以英語的"with"為主),則可被分析成把「個體」映射為「高階函項」的函項,即函項集合U → (Power(U) ∪ Power(U2) ∪ ... → Power(U) ∪ Power(U2) ∪ ...)中的元素。根據此一分析,語句
便可以表達為以下「三分結構」(在下式中,s代表"the stick"):
請注意在上式中,WITH首先作用於U的元素x,所得結果WITH(x)是一個「高階函項」。接著這個「高階函項」作用於有序對集合BEAT,得到另一個有序對集合WITH(x)(BEAT),而有序對(j, b)屬於這個集合。
利用上述概念,我們還可以表達各種「方式量化結構」,只要在表達式中選用適當的量詞便可以了。舉例說,前面包含「全稱方式量詞」"chiel"的語句(1)便可表達為以下「三分結構」(在下式中,t代表"la titolon bravulo"):
請注意由於上式中的第二論元是第一論元的真子集,上式可以改寫為
上式的意思是「方式論域」MANN等同於約翰用來取得「英雄」稱號的方法的集合,這正是語句(1)的意思。
「方式量化結構」也可表現為「方式介詞 + 量化名詞組」的形式,例如以下語句:
由於上句僅包含一個量詞"(at least 2)",這個量詞應取最寬域,因此上句應被表達為以下「三分結構」:
比較一下(3)和(5),我們發現該兩式的量化對象各有不同:(3)以「方式論域」作為量化對象,這是因為語句(1)的"chiel"是在狀語的層面進行量化;(5)則以「個體論域」作為量化對象,這是因為語句(4)的"at least two"是在「介詞賓語」的層面進行量化。
最後談談「方式論域」的特點。跟其他論域不同,「方式論域」是一個高度受限制的論域,這是因為在日常語言對「方式」概念的使用中,我們不會抽象地談論「方式」,而總是談論達成某一具體行為的方式。以語句(1)為例,該句的語義雖然是「約翰用盡各種方法以得到『英雄』的稱號」,但這裡所指的「各種方法」(亦即「方式論域」的元素)應只包括各種可能得到「英雄」稱號的合理方法,而不包括那些不相干或不合情理的方法。由此可見,我們應把「方式論域」理解成一種「局部」(Localized)概念,即不同命題對應著不同的「方式論域」。
表1還有一列以-al結尾的「原因相關詞」,用來表達"for some reason"、"for no reason"、"why"等意思。跟「方式」概念相似,這裡所指的「原因」概念亦包含多個略有不同的意思,除了人們一般理解的「原因」(Cause)外,還有「理由」(Reason)、「目的」(Purpose)、「結果」(Result)等範疇。這些意思跟「原因」的細微差異在於:「原因」是指引起某件事情的條件或原理;「理由」是指用來證實、支持某個論點的理據;「目的」是指產生某種行為的意圖(而且這種意圖不一定是已實現的,所以表達「目的」的句子常以將來時或不定式表示);而「結果」跟「原因」的差異則在於兩者的側重點不同,前者側重表達「因果」關係中的「果」,後者則側重表達「因」。儘管有上述差異,我們仍可把上述多個範疇統一為一個「原因論域」(Causal Domain,以下用C表示),並把「原因/理由/目的/結果」統稱為「原因」(註11)。
我們也可以仿照上一小節的做法,引入一個函項Cause(p),這個函項的論元是命題變項p,其輸出值則是在「原因論域」C中使命題p為真的「原因」組成的集合。利用上述函項,我們便可以把以下英語和世界語語句
| =「約翰無緣無故做此事。」 |
表達為以下三式(在下式中,e代表"the exam";clazy則代表"laziness",它是「原因論域」C上的某個元素):
請注意上面第一和第二句的差別,第一句表示「懶惰」是導致「John考試不及格」的眾多原因之一,而第二句則表示「懶惰」是導致「John考試不及格」的(唯一)原因,上述差異表現為該兩句的表達式須使用不同的量詞。
以上所述只是對「原因」的一種形式表達,以下提供兩種有關「原因」概念的語義解釋。Lewis利用他對「反事實條件句」的分析(詳見《廣義量詞系列:模態量化結構》),把「原因」的語義歸結為一種「模態量化結構」。具體地說,Lewis提出把「直接原因」理解為雙向的「反事實條件句」,即把「p是q的直接原因」解釋為
其中p □→ q代表「反事實條件句」"If p, then q"。上述「直接原因」的定義可作為一般「原因」的定義的基礎,方法是把「原因」理解為由「直接原因」構成的序列,即把「p是q的原因」解釋為:存在一個命題序列p1 ... pn (n ≥ 0)使得「p是p1的直接原因」、「pn是q的直接原因」並且對所有1 ≤ i ≤ n − 1,都有「pi是pi+1的直接原因」。
除了上述解釋外,Talmy在Toward a Cognitive Semantics一書中提出的「動力圖式」(Force Dynamics Schema)是對「原因」的另一種解釋模式。由於「動力圖式」不僅適用於表達「原因」,也適用於表達「讓步」(Concession,即「雖然」所表達的意思),為使討論更具廣泛性,以下將把「原因」概念擴大為「因素」(Factor)概念,從而把「原因論域」推廣為「因素論域」(Factor Domain,以下用F表示)。「因素」跟「原因」的區別在於,「因素」只表達一種不一定能化為現實的因果可能性,而「原因」則表達已成現實的因果關係。
我們把因果關係看成兩個方向相反的力(「推動力」與「靜摩擦力」)作用於一個靜止物體O的過程(註12),「推動力」試圖令O移動,「靜摩擦力」則阻止O移動。兩種力量角力的結果取決於兩者的大小,當「推動力」大於「靜摩擦力」時,O最終會移動;當「推動力」等於「靜摩擦力」時(註13),O最終保持靜止不動。我們可以把上述的「推動力」和「靜摩擦力」表達為方向相反的一對向量。在力學上,兩個力量的角力結果等於代表這對力量的向量的「合向量」(Resultant Vector),「合向量」的方向取決於各個力量的相對大小。
現在讓我們看如何用向量表達以下兩句的語義:
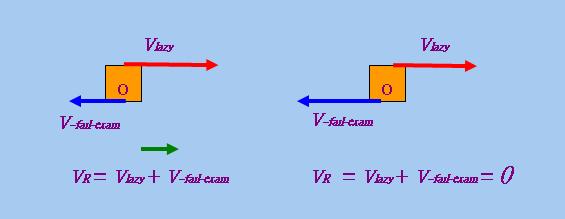
在上述兩句中,(6)表達「原因」,(7)表達「讓步」。現在讓我們把以上兩句的「主體」"John failed the exam"看成靜止物體O可能移動的方向,不妨把這個方向定為水平向右的方向,那麼以上兩句的「因素」"he was lazy"便可以表達為向右的向量vlazy,這個向量代表「推動力」,它試圖令O移動,即導致John在考試中不及格。此外,我們還有一個向左的向量,這個向量代表「靜摩擦力」,它阻止「John不及格」成為事實。請注意以上兩句並沒有說明是哪些因素阻止「John不及格」成為事實,但我們可以憑常理推斷大概存在哪些因素(例如「John運氣好」、「試題太淺易」等),因此我們把這些因素的合力表達為一個向左的向量v~fail-exam。把上述兩個向量相加後所得「合向量」vR的方向反映了兩個力量角力的結果。下圖顯示角力的兩種可能結果:

上面左圖顯示|vlazy| > |v~fail-exam|的情況。在此情況下,vR為向右的向量,物體O會向右移動,這代表John懶惰的因素足以導致John不及格,此即語句(6)所要表達的結果。上面右圖顯示|vlazy| = |v~fail-exam|的情況。在此情況下,兩個向量剛好互相抵消,vR等於「零向量」0,物體O保持不動,這代表John懶惰此一因素還不足以導致John不及格,此即語句(7)所要表達的結果。如前所述,我們規定vlazy與v~fail-exam互為反向向量,並且後者的長度不得大於前者, 這一點可以表述為
在上式中,k是一個不小於1的實數,它的大小決定了vlazy與v~fail-exam這兩個向量的相對大小。根據以上討論,我們可以把語句(6)和(7)表達為
利用上述向量概念,我們容易表達「因素論域」。正如「方式論域」那樣,「因素論域」也是「局部」概念,即對應於不同命題有不同的「因素論域」。以語句(6)和(7)為例,相關的「因素論域」F應只包括那些可能導致John不及格的因素,而不包括那些與John考試不相干的因素。根據上述的向量概念,這些因素可表達為與v~fail-exam反向並且其長度不小於|v~fail-exam|的向量,即
而「原因論域」C則是F的子集,這個子集包含那些與v~fail-exam反向並且其長度大於|v~fail-exam|的向量,即
在語言的使用上,有時我們需要突出某個句子成分,這個被突出的成分可以是主語或賓語,也可以是定語、狀語等,被突出的成分可以是「個體論域」以外其他論域的元素。在自然語言中,最常用來突出某個句子成分的方法是使用「焦點結構」(Focus Construction),因此「焦點結構」與本節討論的各種「相關詞論域」有密切關係。在自然語言中表達「焦點」的常見方法是使用「語調」,即把句子中的「焦點」讀重一點。在文字上,我們無法表達這種「重讀」,但語義學界通常使用符號[ ]F把「焦點」括出來。以上面的語句(3)為例,如果我們想以該句表達的「方式」作為「焦點」,那麼我們可以把該句寫為
除了使用語調外,自然語言中還有一些特殊的詞匯或結構可用來表達「焦點」。由於本文的重點並非討論「焦點結構」,所以以下僅介紹一種常見的「焦點結構」,這種「焦點結構」就是含有"only"的結構。《廣義量詞系列:基本單式量詞》的表3顯示,"only"是一個「<1,1型>量詞」,其真值條件可表達為
筆者認為,英語中包含"only"的「焦點結構」也體現了這同一個"only"的基本語義。試考慮以下語句:
上句的焦點是動詞"borrowed"。由於這句是以動詞(在邏輯學上常表達為「謂詞」)作為句子談論的對象,所以上句應被看成「謂詞論域」上的量化句。這樣,根據上面"only"的真值條件,我們可以把上句表達為以下「三分結構」和集合論表達式(在下式中,PRED為包含各種動作行為的「謂詞論域」,b代表"the book"):
在上式中,{P ∈ PRED: P(j, b)}代表「John對那本書所做的事組成的集合」,因此上式的意思是,「借」是John對那本書唯一可能做了的事。但請注意,上式只表達了一種可能性,即如果John對那本書做了甚麼事的話,那麼這種事便只可能是「借」,但並沒有斷定John必定借了那本書。可是從語用上看,語句(8)又應含有John確實借了那本書的意思,否則這句話就是無的放矢。根據語言學家的研究,含有"only"的「焦點結構」的全部語用內容應包含「斷言」(Assertion)和「預設」(Presupposition)兩部分,其中"only"的基本語義就是其「斷言」。由此可見,上式只反映了語句(8)的「斷言」,並未反映該句的「預設」。
所謂「預設」,就是指某語句的基本假設,其特點為即使把該語句否定,「預設」仍然成立。對於含有"only"的「焦點結構」而言,其「預設」部分一般就是句中略去"only"的那部分,例如語句(8)的「預設」就是"John borrowed the book"。容易看到,若把(8)換成其否定
預設"John borrowed the book"仍然成立,即無論John是否只借了那本書,「他借了那本書」此一事實都是真的。因此,我們可以把語句(8)的「預設」表達為以下「三分結構」和集合論表達式:
把上面表達「斷言」的(9)和表達「預設」的(10)合起來,我們便得到以下集合論表達式:
上式的意思是,John借了那本書,而且除了「借」以外,沒有對那本書做其他事,這反映了語句(8)的完整語用內容(註14)。
「度量」(Measure)是自然語言表達「量」的重要方式。在日常語言中,某些性質,如「長」、「重」、「熱」等物理量,都有明確和公認的計量標準,可以用某個實數代表該性質所達到的量。由此可見,「度量」實際上是前述「數量論域」的一種運用。不過,創立「向量空間語義學」的學者Winter等人利用向量的概念詮釋表達「度量」的語句,從而大大豐富了「度量」的語義學內容;而且筆者認為,我們可以把「度量」概念推廣引伸至「程度」、「比較結構」、「序數詞」、「不可數名詞」、「部分-整體關係」等多種語言結構,因此筆者特闢本節專門討論「度量」的語義問題。
以下借用Winter的Measure Phrase Modification in Vector Space Semantics和Faller的Dimensional Adjectives and Measure Phrases in Vector Space Semantics文章中的某些概念介紹「度量」的向量表達法。簡言之,這個方法把「度量」表達為向量,故可稱為「度量向量」(Dimensional Vector),並把在某一應用中所有「度量向量」組成的集合稱為V。由於「度量」是一維概念(即只有增大和減小這兩個方向而沒有其他方向),我們假設V中的元素全都是以「原點」為「起點」,垂直向上或向下的向量或「零向量」。取定某一長度的向量作為「單位向量」u後,我們便可以把V中的元素表達為r • u,其中實數r是向量的「模」(亦即長度),它可用來代表「度量」的數值。由於在具體應用中,「度量」的數值一般都有一定的取值範圍,我們把這個取值範圍記作R。舉例說,假設我們是在談論成人的高度,並以「m」為單位,那麼V中的「單位向量」u便代表1 m的高度,而其他向量則代表其他高度,例如一個長度兩倍於u的向量(即2 • u)便代表2 m的高度。此外,如果我們假設所有成人的高度都不小於0.7 m且不大於3 m,那麼我們有R = [0.7, 3],並且
換句話說,V的元素是所有長度介乎[0.7, 3]的向量,這些向量代表所有可能的成人高度。
我們可以利用上述概念表達各種涉及「度量」的語句,以下首先考慮「絕對度量」(Absolute Measure),這種「度量」的例句如:
Winter把「度量形容詞」(Dimensional Adjective)區分為「正向形容詞」(Positive Adjective)和「負向形容詞」(Negative Adjective)兩種,前者的例子如「高」、「胖」、「重」等,後者的例子如「矮」、「瘦」、「輕」等。Winter並且假設存在一個可能隨語境而變化的「度量標準」s,凡不小於s的「度量」都可用「正向形容詞」來表達,否則便要用「負向形容詞」來表達。這樣,「高」、「矮」等表達「度量」的形容詞便都可表達為「度量向量」集合(以下集合的名稱使用粗體是為了強調這些集合的元素是向量,以區別於由個體組成的集合或形容詞):
當然,由於「高」、「矮」等屬於模糊概念,上述定義只能被看做一種近似表達法。下文筆者還會討論如何借助「模糊數學」的方法表達這些模糊概念。
由於上面的TALL(e(X'))是向量集合而"John"是個體,我們不能直接對兩者進行比較。為此,我們必須進行「類型轉換」。筆者仿照Faller的文章引入一個「度量函項」Dim[N](u),其作用是把個體u映射為u相對於「度量名詞」N的「度量向量」,例如Dim[HEIGHT](j)便代表John相對於HEIGHT的「度量向量」,即其長度等於「John的高度」的向量。利用這個函項,我們便可以把上面的語句(11)表達為
利用向量的概念,我們很容易表達上面帶有「相交修飾語」"1.3 m"的語句(12)。正如筆者在《廣義量詞系列:空間量化結構》的表1所示,我們可以把這類「相交修飾語」表達為「度量向量」集合{r • u: r = 1.3}。不過,這裡存在一個問題。在很多自然語言中,當「正向形容詞」與「相交修飾語」或「疑問詞」連用或變成「度量名詞」時,常會出現一種特殊的語義擴大現象,就是「正向形容詞」的語義擴大至包括「反向形容詞」的語義,從而變成一種語義「中立」的形容詞。以語句(12)為例,該句的"tall"其實不僅指可稱為「高」的高度(例如1.8 m),而是涵蓋一切在R範圍內的高度。事實上,以成人的平均高度來說,1.3 m應算是「矮」。由此可見,語句(12)中的"tall"其實是語義「中立」的。同樣,語句(13)中的"tall"並不意味著發問者預設John是高的,它實際上也是語義「中立」的。請注意「反向形容詞」並無類似的語義擴大現象,這些形容詞在任何情況下都不能涵蓋「正向形容詞」的語義,因此語句(14)中的"short"意味著發問者預設John是矮的。
基於以上討論,我們必須把上述TALL定義中有關「標準」s的條件刪去,從而得到以下定義:
上式中的TALL(e(X'))帶有下標n,表示這個TALL是語義「中立」的形容詞。現在,根據「相交修飾語」的性質,我們便可以把(12)表達為
| Dim[HEIGHT](j) | ∈ TALL(e(X'))n ∩ {r • u: r = 1.3} |
| = {1.3 • u} |
利用筆者以往介紹「疑問量詞」的知識,我們可以把語句(13)和(14)分別表達為
「相對度量」(Relative Measure)表達「度量」之間的比較,典型的例句包括以下的「比較句」:
「向量空間語義學」使用「定位向量」(Located Vector)的概念來表達「相對度量」,「定位向量」就是不一定以「原點」為「起點」的向量。為了方便以下討論,我們假設所有「定位向量」都是垂直向上或向下的,並把以點p為「起點」的「單位定位向量」記作up。為讓讀者易於明白,以下首先解釋如何用「定位向量」表達語句(15)。從直觀上說,該句的意思就是存在一個代表John高度的「度量向量」Dim[HEIGHT](j),其長度大於代表Mary高度的「度量向量」Dim[HEIGHT](m)。我們亦可以從另一個角度理解該句,Dim[HEIGHT](j)等於Dim[HEIGHT](m)與另一個「定位向量」w的「向量和」,這個w以Dim[HEIGHT](m)的「終點」為「起點」,因此亦可寫作x • uE-point(Dim[HEIGHT](m)) (其中x為實數),其方向指向上(即x > 0)(請參看下圖)(註15):
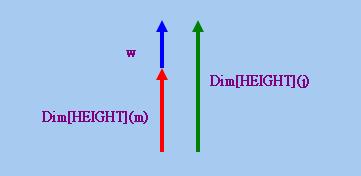
請注意這裡的「w指向上」並非所有「比較句」的通則,在某些情況下,我們需要規定「w指向下」。以下筆者借用Winter一文中的概念作為確定w方向的條件(略作修改),這個條件須用到兩個函項:Sign和Polarity,前者以實數x為論元,其輸出值為1或−1,分別代表x是正數或負數;後者則以「度量形容詞」A為論元,其輸出值為1或−1,分別代表A是「正向形容詞」或「反向形容詞」。利用上述兩個函項,我們便可以把上述確定w方向的條件表述為
由於TALL是「正向形容詞」,把TALL代入上式中的A後,得Polarity(TALL) = 1,由此得Sign(x) = 1,即x > 0,亦即w指向上。基於以上分析,我們可以把語句(15)表達為
| Dim[HEIGHT](j) | ∈ {v ∈ V: v = Dim[HEIGHT](m) + x • uE-point(Dim[HEIGHT](m)) ∧ Sign(x) = Polarity(TALL)} |
| = {v ∈ V: v = Dim[HEIGHT](m) + x • uE-point(Dim[HEIGHT](m)) ∧ x > 0} (20) |
上述原理亦可應用於語句(16),但須作出適當調整。根據該句,「定位向量」w應以Dim[HEIGHT](j)的「終點」為「起點」,其「終點」應等於Dim[HEIGHT](m)的「終點」。但由於|Dim[HEIGHT](j)| > |Dim[HEIGHT](m)|,所以w應指向下(請參看下圖)。
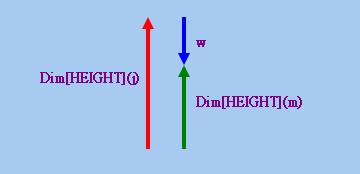
請注意由於SHORT是「反向形容詞」,Polarity(SHORT) = −1,所以我們可以根據等式(19)推得w指向下。由此可見,等式(19)其實同時涵蓋了A為「正向形容詞」或「反向形容詞」的情況。這樣,我們只需把上面(20)中的個體j和m對調,並把Polarity(TALL)改為Polarity(SHORT),便可得到語句(16)的表達式。
至於語句(17),由於"less tall"在語義上等同於"shorter",該句的表達式應與(16)的表達式相同,即「定位向量」w應指向下。但由於(17)中使用的是「正向形容詞」"tall",我們必須把等式(19)修改為
這樣我們便有兩個確定w方向的條件:(19)和(21),前者適用於含有"more"或"-er"的「比較句」,後者適用於含有"less"的「比較句」。請注意由於Polarity(SHORT) = −Polarity(TALL),語句(16)和(17)將有相同的表達式,而這反映了該兩句的同義性質。
最後討論語句(18),這句含有「相交形容詞」"0.1 m"。跟前面的做法類似,我們可能想把代表"0.1 m"的集合{r • u: r = 0.1}與(20)中的集合{v ∈ V: ...}相交,但這是不正確的,因為0.1 m不是Dim[HEIGHT](j)的長度,而是w的長度。因此,正確的表達式應為
至於如何把上式表達為兩個集合的交集,這涉及頗複雜的問題,這裡不再深入討論。
在上一小節筆者討論了某些性質的「度量」問題,這些「度量」都有明確和公認的計量標準(例如用於「長度」的「m」),可以表示為實數。但是更多的性質,如「美」、「好」、「可靠」等,並無客觀的計量單位,而且具有模糊性,但這卻無礙於人們就這些性質進行比較。由此可見,在說話者心目中,這些性質其實也存在某種量值,儘管這種量值可能是很主觀的。因此,筆者假設模糊性質也可表達為「度量函項」。
在自然語言中,除了使用精確的「實數值」(即「度量函項」的值)來刻劃某個體在某性質上的程度外,也常常使用模糊的「語言值」來擔當相似的功能。舉例說,設John的高度為2米,我們除了可以用精確的語言說"John has a height of 2 m."外,也可以用模糊的語言說"John is tall."。由此可見,「語言值」與「模糊集合」(Fuzzy Set)概念有密切關係。在模糊數學中,「隸屬度函數」μ[S](x)可用來表達某一個體屬於某一「模糊集合」S的程度(這裡把「性質」表達為一個「模糊集合」),這個函數的輸入值(又稱「參項」Parameter)是x,可視乎所刻劃的性質而取適當的「度量」值,輸出值則是區間[0, 1]上的實數,數值越大代表x屬於S的程度越高。以性質「高」為例,我們可以把它表達為「模糊集合」TALL(e(X')),其「隸屬度函數」為μ[TALL(e(X'))](x),其中x可以取論域中個體的「高度」。利用上述概念,我們便可以把語句
的真值表達為
在日常語言使用中,當我們無需或無法使用精確語言時,便有必要使用模糊語言。可是如果只單純使用代表「模糊集合」的詞語(例如"tall"、"reliable"等),又未免過於粗疏。為了在上述兩種極端情況中求取平衡,我們可以使用「程度修飾語」(Degree Modifier)使我們的模糊語言變得精細一點。以下筆者將集中討論那些具有最高和最低程度的性質(例如"reliable"、"full"等),並假設這些性質的「度量函項」在區間[0, 1]上取值,其中0和1分別代表最低和最高程度(註16)。請注意這種「度量函項」儘管在表面上跟「隸屬度函數」非常相似(兩者都在[0, 1]上取值),但兩者具有很不相同的性質。當前者取值為1時,代表「達到最高程度」;但當後者取值為1時,僅代表「達到某個閾值」。
「程度修飾語」可分為幾類,本文只擬討論其中兩類。第一類「程度修飾語」包括"completely" 、 "partially"、"half"、"to a certain extent"、"to a certain extent not"、"not at all"等,這類修飾語所表達的意義相當於某種比例(例如"completely"便相當於100%),故可稱為「比例修飾語」(Proportional Modifier)。請注意「比例修飾語」所表達的意義是不模糊的,所以我們可以直接使用「度量函項」來表達含有這類修飾語的語句。此外,由於「比例修飾語」具有副詞的性質,我們應根據它們對「度量形容詞」的作用來確定它們的語義。下表列出各個「比例修飾語」的真值條件(在下表中,A代表「度量形容詞」,N代表與A相應的「度量名詞」,u代表個體):
| 論元結構 | 真值條件 |
|---|---|
舉例說,由於語句
可以抽象為
根據上表,上句的真值條件為
第二類「程度修飾語」表達某種模糊程度,故可稱為「模糊限制語」(Fuzzy Hedge)。這類修飾語可按其表達程度的高低排成以下序列:"extremely"、"very"、"rather"、"slightly"、"a bit"、"scarcely"等 (註17)。由於「模糊限制語」所表達的意義是模糊的,所以應使用「隸屬度函數」刻劃其意義。此外,由於「模糊限制語」也具有副詞的性質,它們應具有與「比例修飾語」相同的論元結構,而包含「模糊限制語」的語句的真值則由適當的「隸屬度函數」給出。舉例說,含有"very"的語句的真值應為
請注意F1是以「度量函項」的值|Dim[N](u)|作為輸入值的函數,我們可以把這個函數定為(以下的函數跟《廣義量詞系列:模態量化結構》中的公式(7),即VERY-LIKELY(e(X'))的「隸屬度函數」具有相同的形式):
| 0, | if 0 ≤ x ≤ 0.8 | |
| F1(x) = | (x − 0.8) / 0.1, | if 0.8 ≤ x ≤ 0.9 |
| 1, | if 0.9 ≤ x ≤ 1 |
利用上述定義,我們便可以把語句
的真值定為
設John的「可靠度」(即|Dim[RELIABILITY](j)|)為0.85,那麼上句的真值便是0.5。
以上所述的「度量」是定義於個體上的概念,但在自然語言中,我們也可以討論動作/行為的「度量」,例如語句
便涉及度量「John跑步的速度」。因此我們需要定義新的「度量函項」Dim[N](P(u)),其中P代表謂詞,例如「John跑步的速度」便可以表達為|Dim[SPEED](RUN(j))|。利用此一函項,我們可以把上句的真值表達為
請注意在上式中,QUICKLY本身不是「模糊集合」,而是「方式論域」的元素(即一個「高階函項」),它作用於RUN後,所得結果QUICKLY(RUN)才是「模糊集合」。
類似地,前述的「程度修飾語」本是定義於「度量形容詞」上的概念。現在我們把這個概念推廣,使之也適用於「方式副詞」。以"very"為例,這個「程度修飾語」除可修飾「度量形容詞」外,亦可修飾「方式副詞」。我們可以把含有「very + 方式副詞」的句子的真值定為:
在上式中,M代表「方式副詞」,P代表謂詞,N代表與M相應的「度量名詞」,F1則為上一小節定義的函數。請注意這裡也須假設上式中的「度量函項」乃在區間[0, 1]上取值。利用上式,我們便可以把語句
的真值定為:
在3.2和3.3小節,筆者已討論過「比較結構」(Comparative Construction),在該兩小節筆者重點討論兩個量值之間的比較。在本小節筆者將從另一個角度理解「比較結構」,特別著重研究「最高級」(Superlative Degree)和「比較級」(Comparative Degree)所表達的意義。「最高級」和「比較級」是自然語言中「級」此一語法範疇的兩個表現形式,在英語中分別以"-est"/"most"和"-er"/"more"表示。這兩個「級」都是表達在某一特定論域內個體之間就著某一性質進行比較的結果。從某一角度看,我們可以把「最高級」和「比較級」看成分別對應於「全稱量詞」和「存在量詞」。這是因為「最高級」表達論域中某個體在符合該性質的程度方面高於所有其他個體,而「比較級」則表達某個體在符合該性質的程度方面高於至少一個他以外的個體。
現舉一個具體的例子以作說明。設論域U為人的集合,CLASS為John那一班全體學生組成的集合,並且我們以John為基點,只考慮John與同班同學比較的情況,因此我們所關注的集合是CLASS–{j}。我們還假設論域中沒有兩個人的高度相同。這樣,我們便可以保證班中不會出現兩個同為最高的學生。基於以上定義和假設,語句
便可以表達為以下三分結構:
即班中除了John以外的所有學生都較John矮,此即John最高的意思。同理, 語句
可表達為
請注意在上述「比較結構」的三分結構式Q(A)(B)中,A和B分別對應著「比較結構」中的不同語義部分,其中A對應著「比較範圍」(例如上句中的CLASS–{j}表示比較是在John那一班的範圍內進行),而B則代表「被比較的性質」(例如上句中的{x ∈ U: |Dim[HEIGHT](j)| > |Dim[HEIGHT](x)|}表示被比較的性質是高度)。
前面討論的「比較結構」Q(A)(B)中的Q只體現為"every"和"some"這兩個量詞,現在如果我們以其他量詞作為Q,將可得到更多類型的「比較結構」。舉例說,如果以"most"作為Q,那麼三分結構
便代表以下語句:
「數詞」(Numeral)一般可分為「基數詞」(Cardinal Numeral)和「序數詞」(Ordinal Numeral)這兩種,前者表達數目多少,例如英語的"one"、"two"、"hundred"、"thousand"等;後者表達次序,例如英語的"first" 、 "second"、"hundredth"、"thousandth"等。「基數詞」是「數量論域」的元素,在前面已討論了很多,本節集中討論「序數詞」。
筆者認為,「序數詞」與「比較結構」存在密切關係,因此可不妨借用「比較結構」的形式化方法來表達「序數詞」。事實上,「序數詞」常可出現於「比較結構」中,作為「最高級形容詞」的修飾語,例見以下語句:
為了與上一小節的表達式保持一致,我們可以把上句理解為「除了一名同學外,John較班中所有其他學生都高」。由此我們建立了「序數詞」與「例外結構」和「比較結構」的聯繫,即上句可表達為以下三分結構:
一般地,語句
可以表達為
「序數詞」並不局限於表達性質之間的比較,它們更常用於表達空間和時間位置,例見以下語句:
為表達上面第一句,我們可以使用表達空間關係的二元函項"(in front of)",這個函項以兩個點集合A和B為論元,(in front of)(A, B)表示A在B之前。至於上面第二句,則可使用筆者在《廣義量詞系列:時間量化結構》中介紹的函項Time。利用上述兩個函項,我們便可以把以上兩句表達為以下三分結構(在下式中,QUEUE和STUDENT分別代表正在排隊的人和學生組成的集合):
請注意在上面第一式中,由於"(in front of)"是以點集合為論元的函項,而j和x卻是個體,我們必須使用《廣義量詞系列:空間量化結構》中介紹過的函項Loc把j和x轉化為這兩個個體所在位置的點集合,然後才能把"(in front of)"作用於這兩個點集合。
最後討論"first"和"last",這兩個詞一般不能出現於「比較結構」,但卻可用來表達空間和時間位置,它們的角色類似「最高級形容詞」(請注意這兩個詞都是以"-st"結尾,正好與「最高級」詞尾"-est"吻合)。舉例說,以下兩句
便可分別表達為
由此我們建立了"first"和"last"與量詞"every"和"no"的聯繫。
Cresswell的"The Semantics of Degree"一文是研究與「度量」有關的語義問題的早期文獻,上面3.1小節介紹的把「度量」處理成向量的方法可以說是對Cresswell文中某些概念的改良和發展。Cresswell的文章除了討論「度量」的表達形式外,還把這種表達方式推廣至「可數名詞」(Count Noun)和「不可數名詞」(Mass Noun),以表達這兩種名詞的量。由此可見,「度量」與「可數名詞」和「不可數名詞」的量其實有某種相通之處。以下沿襲Cresswell一文的精神,把前面有關「度量」的某些概念推廣應用於這兩種名詞。
「可數名詞」的量可分為「絕對量」和「相對量」兩種,「絕對量」就是代表該名詞的集合的基數。利用前面3.1小節介紹的概念,我們可以用向量Dim[MODULUS](A)代表集合A的基數,即
在上式中,MODULUS代表集合元素的數目。至於「可數名詞」的「相對量」,則是指代表該名詞的集合基數相對於其母集基數的比率。例如設A ⊆ B,那麼向量Dim[PROPORTIONB](A)便代表A的基數相對於B的基數的比率,即
上述概念亦適用於「不可數名詞」。由於「不可數名詞」不能像「可數名詞」那樣一個個的計數,我們不能把它們表達為一般的集合,這是因為對於「不可數名詞」所指稱的事物而言,並不存在最小的個體可作為集合的元素(註19)。不過,Bunt在Mass Terms and Model-Theoretic Semantics一書中提出了「整體」(Ensemble)的概念,可用來刻劃「不可數名詞」。本文不擬闡釋有關「整體論」(Ensemble Theory)的詳細內容,只想指出「整體」跟「集合」兩者都是由多個部分組成,但「整體」跟「集合」不同,不一定存在最小的部分(即個體/元素),因此「整體論」是以「包含」(⊆)而非「屬於」(∈)關係作為基本關係(註20)。「集合論」中與「包含」關係有關的各條定理,在「整體論」中繼續有效,由此可見「整體論」是對「集合論」的推廣。
在「整體論」的框架下,我們可以繼續使用某些量詞,但要作出新的詮釋,試看以下語句:
請注意我們不能把上句簡單表達為
這是因為被John喝下的東西(以及WATER)是不可數的,不能簡單地表達為集合,而應表達為一個「整體」。構成這個「整體」的單位不是「元素」,而是「部分」(請注意「部分」在本質上也是「整體」)。這些部分大小不等,可以小至只包含一滴液體,也可以大至包含當前論域中的所有液體,而且各個部分之間可以存在「包含」關係。這些「部分」合起來構成以下集合:
請注意在上式中,我們使用「⊆」而非「∈」,因此x不是個體,而是「部分」。對這個集合中的「部分」進行「合併」(Merge)運算(註21),便得到以下這個包含著所有使DRINK(j, x)為真的「部分」的最小「整體」:
Bunt亦把上式寫為
請把上式與一般集合的表達形式{x ∈ U: ...}加以比較。利用上式,我們便可以把語句(22)表達為
我們也可以為「不可數名詞」引入兩種「度量」。我們雖然不能點算「不可數名詞」的個數,但卻有各種方法計量這些物質的數量,例如體積、質量、摩爾(Mole)、容量等,這樣我們便可使用函項Dim[QUANTITY]來表達「不可數名詞」的「絕對量」。例如我們可以把語句
表達為(我們假設下式中向量的單位向量代表「ml」):
同樣,我們也可以用Dim[PROPORTIONB](A)來表達A的量相對於B的量的比率(這裡A和B為「整體」,並且A是B的一部分),即
舉例說,語句
便可表達為
請注意在上式中,筆者使用X ∩ WATER來代表上句中的"the water",這是因為John所喝的水不是世界上任何水,而是在當前語境中凸顯的那些水。
在日常語言中,有時我們會把某些個體看成由各個部分組成的整體,例如在語句
中,John的外部身體便被看成由各個部分組成的整體。有些物件/團體由多個部件/成員組成,例如"furniture"由椅子、桌子等組成,"family"由家人組成;但在某些場合下,這些物件或團體可被視為整體而非部件/成員的集合,例如當我們說
時,我們是把"furniture"和"family"視為整體。這時物件/團體與部件/成員的關係是整體與部分的關係,本文把這種關係稱為「部分-整體關係」(Part-Whole Relation)。
從某個角度看,「部分-整體關係」有點類似包含「複數可數名詞」的語句。但筆者認為,不宜對這些語句作出這樣的理解。以語句(25)為例,當說話者說出這句時,他的著眼點並非John身體上的一個個部位,而是著眼於John濕了的部分相對於他全身的比率。事實上,我們應把這種結構處理成上一小節介紹的「不可數名詞」,因為「不可數名詞」的特點正是不能切分為一個個元素(請注意前述的"furniture"在英語中正是表現為「不可數名詞」)。基於以上討論,我們可以沿用上一小節的概念,把"John's body"看成「整體」,並像上面的(23)那樣把語句(25)表達為
請注意在上式中,[x ⊆ JOHN'S-BODY: SOAKED(x)]實際上是JOHN'S-BODY的部分,所以上式又可以改寫為
我們也可以沿用上一小節介紹的函項Dim[PROPORTIONB](A)(見公式(24),但在此例子中須把該公式中的QUANTITY理解為John外部身體上某些部分的面積),這樣我們便可以把(25)表達為
筆者至此已介紹了多種「廣義量化結構」,所涵蓋的領域包括「個體論域」、「時間論域」、「可能世界論域」、「命題論域」、「空間論域」(包括「點域」和「向量域」)、各種「相關詞論域」以及由「度量」概念派生出來的多種結構,這足以證明「量化」是自然語言中一個極重要的現象。由於自然語言具有遞歸性、組合性的特點,上述各種論域下的量化結構有時還可出現於同一句中,形成「混合量化結構」(Hybrid Quantified Structure)。不過,由於「混合量化結構」涉及多種論域,往往存在「轄域」的問題,即在表達式中哪一個論域取「寬域」,哪一個論域取「窄域」的問題。舉例說,以下語句
看似簡單,但其實已涉及三個論域:「個體論域」、「時間論域」和「可能世界論域」。在這裡,我們假設在上句中,「可能世界論域」取最寬域,「時間論域」次之,「個體論域」則取最窄域。基於以上討論以及筆者在以往各章介紹的相關內容,我們可以把上句表達為
在上式中,|BOOK ∩ {x ∈ U: RETURN(j, x)}| ≥ 2表示John歸還至少兩本書;Time(...) ⊆ tomorrow(X')表示上述還書行為發生於明天;WD**是「極優可能世界集」,WD** = World(...)則表示明天必須發生上述還書行為。
「混合量化結構」的「轄域」可能會隨著所用詞匯的位置分佈、所用的語言結構、句子焦點的所在位置等因素而變化,由於這將涉及很複雜的問題,討論只能到此為止。


